Going Beyond Woodward and Hoffmann's Electrocyclizations and Cycloadditions: Sigmatropic Rearrangements

Abstract

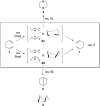
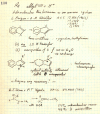
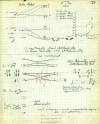
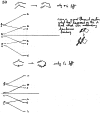
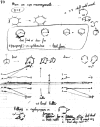
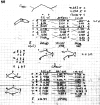
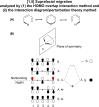
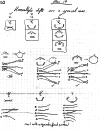
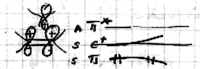
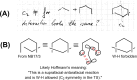
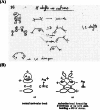
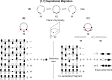
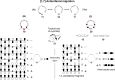
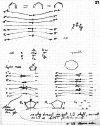
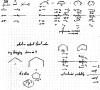
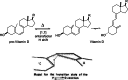
On June 1, 1965, R. B. Woodward and Roald Hoffmann published their third communication in the Journal of the American Chemical Society in which they applied orbital symmetry control to explain the mechanism of a wide variety of valence isomerizations that they termed "sigmatropic reactions." This publication reveals the research trajectory taken by Hoffmann from which this portion of the no-mechanism problem was solved. Hoffmann used five different quantum chemical tools, all based on either extended Hückel theoretical calculations or frontier molecular orbital theory, in his research. Hoffmann's laboratory notebooks and his three draft manuscripts along with Woodward's four subsequent drafts have survived the past 59 years and provide an excellent window into the thinking and manuscript-writing processes used by these Nobel laureates in February-April 1965.

Keywords: Conservation of Orbital Symmetry; Cope reaction; Frontier Molecular Orbital Theory; Woodward-Hoffmann rules; sigmatropic reactions.

Figure 1

(Left to right) William von E. Doering and Michael J. S. Dewar, Hickrill Chemical Research Foundation, New York, ca. 1955.

Figure 2

(Left to right) Roald Hoffmann, Herman Bloch (chair of the Board of Directors of the American Chemical Society), Mrs. Harriet Cope, and R. B. Woodward, at the first Cope Award presentation, 166th National Meeting of the American Chemical Society, Chicago, I, August 28, 1973. Arthur C. Cope died on June 4, 1966. It is fitting that Woodward and Hoffmann received the first Cope Award, in that the Woodward‐Hoffmann rules including their well‐described secondary orbital interactions provided the mechanism for the Cope reaction.[ ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ ]

Figure 3

Equations 1–2 are examples of reactions that formally are [3,3] sigmatropic rearrangements.[ ⁹ , ¹¹ , ¹⁶ , ⁴² , ⁴³ ] Eq. 3 is a [1,5] hydrogen shift. The Benzidine rearrangement (eq. 4) has been considered to go through [3,3] and/or [5,5] rearrangements. The σ‐bonds being made and broken in these rearrangements are shown in red font. Citations from the 1960s and earlier.

Figure 4

(Inside the box) Analysis of the Cope reaction of 1,5‐hexadiene (eq. 1 and eq. 5; the horizontal transit) using complexes consisting of two allyl radicals, one of which (4 b) is oriented in a boat conformation and the other (4 c) in a chair conformation. This model was first proposed by Doering and Roth in 1962.[ ¹¹ , ¹⁴ , ⁵⁴ ] (Inside and outside the box) Hoffmann's model included reactions of the complexes of the two allyl radicals that led to cyclohexane 1,4‐diyl (3) and bicyclo[2.2.0]hexane (2) via eq. 6c and eq. 6b, respectively (the vertical transits). For most of his eHT calculations, Hoffmann modified Doering's model for a boat TS by placing the two allyl moieties in parallel planes as in 5).[ ³ , ⁴ , ⁶ ]

Figure 5

R. Stephen Berry, 1962. Berry would later become a leading physical chemist and member of the National Academy of Sciences. Photograph courtesy R. S. Berry.

Figure 6

Kenichi Fukui, ca. 1955. Photograph courtesy Tetsuya Fukui.

Figure 7

Early sigmatropic reactions studied by Hoffmann. (A) Excerpts from Hoffmann's 1964 publication on “Extended Hückel Theory. IV. Carbonium Ions” in which he calculated various properties of protonated ethylene and protonated cyclopropane. The former carbocation structure may be considered the TSs for the hydrogen shift shown in (B; eq. 7) for the protonation of cyclopropane. (C) Excerpt from page 30 of Hoffmann's Laboratory Notebook 17, written ca. April 8, 1965. On this page, Hoffmann constructed simple interaction diagrams for ethyl carbocation and symmetrical protonated ethylene. Compare these interaction diagrams drawn in April 1965 with the protonated ethylene structure in (A) from a manuscript submitted on September 27, 1963.

Figure 8

Classical and nonclassical 2‐norbornyl carbocations and the classical structures of 7‐norbornyl, norbornenyl, and norbornadienyl carbocations studied by Hoffmann in 1963.[ ⁶⁴ , ⁶⁵ ]

Figure 9

(A) Excerpt from page 143 of Hoffmann's Laboratory Notebook 11, ca. early January 1964. Here, Hoffmann recorded Doering's Cope reactions from his 1963 review article on Thermal Rearrangements. (B) Excerpt from page 126 of Hoffmann's Laboratory Notebook 13, July 29, 1964. Hoffmann compared a hydrogen shift in keto‐enol tautomerism as “analogy again to Cope rearrangement.” The keto‐enol rearrangement is formally a [1,3] sigmatropic reaction.

Figure 10

Hoffmann's notes (page 89 of 97 pages) from Douglas E. Applequist's course on small ring carbon chemistry, Harvard, ca. April 1964. Hoffmann recorded several examples of Cope rearrangements and wrote, along with its structure, “also bullvalene”. Applequist cited Doering and Roth's eight page review article on Thermal Rearrangements published in 1963 which consists primarily of examples of Cope rearrangements and an extensive discussion of bullvalene.

Figure 11

Page 130 from Hoffmann's Laboratory Notebook 13, ca. June 1964. On this and the following page of this notebook, Hoffmann listed a series of hydrogen shifts and carbon shifts that can be described as sigmatropic rearrangements. On this page, Hoffmann described the application of various mechanistic tools, including retention or loss of enantiomeric purity and intermolecular or intramolecular reactions. Note the four references at the upper right‐hand corner of this page. The “ACS” does not refer to the American Chemical Society. Rather, it was Hoffmann's shorthand for Acta Chemica Scandinavia. That Nordic chemistry journal ceased publication in 1999 when it merged with the Royal Society of Chemistry's journals for organic and inorganic chemistry. The senior author of the four cited publications on this page is Gören Bergson who brought these sigmatropic reactions to Hoffmann's attention in the very early 1960s.

Figure 12

Excerpts of MIT's C. Gardner Swain's notes of William von E. Doering's lecture at the Tenth Conference on Reaction Mechanisms, Corvallis, OR, June 24–27, 1964.

Figure 13

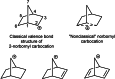
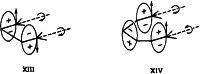
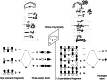
More on the Cope reaction in Hoffmann's laboratory notebooks. (A) Excerpt from Hoffmann's Laboratory Notebook 15, page 45, ca. early September 1964. Hoffmann's reference omitted the page numbers, i. e., pp 2791–2795. Of no relevance to this discussion, a methyl group is accidentally omitted in the middle structure. The first transformation is a Cope reaction; the second is a Conia‐ene reaction.[ ⁸¹ , ⁸² ] (B) Excerpt from Hoffmann's Laboratory Notebook 15, page 116, ca. November 21, 1964. See Hoffmann's note above the arrow, “disrotatory.” He was trying to analyze the Cope reaction using electrocyclization mechanistic thinking and nomenclature. Hoffmann was just then working on the drafts for the first W−H publication on electrocyclizations.

Figure 14

Table XV from Mathieu and Valls's 1957 publication entitled “Le tranfert électronique circulaire dans l′interprétation de certaines réactions de la Chimie organique.” The clustering of (A) a Cope reaction, (B) a [1,5] sigmatropic reaction, and (C) what would eight years later be called an electrocyclization, was quite prophetic by Mathieu and Valls. Had there been a bond between the terminal carbons in (C), this reaction would have been between the two resonance hybrids of Kekulé’s structure of benzene.

Figure 15

Page 127 from Hoffmann's Laboratory Notebook 15, ca. late November to early December 1964. These are Hoffmann's notes from William von E. Doering's seminar at Harvard. Hoffmann imagined a number of other rather exotic Cope reactions on the following laboratory notebook page (not shown here). Note on line 8 of this page, “RBW thinks it's steric course.”

Figure 16

Roald Hoffmann, ca. 1966. Note the pencil and pen pocket protector that was typical of that era. Photograph courtesy R. Hoffmann.

Figure 17

Page 27 from Hoffmann's Laboratory Notebook 16, ca. February 2, 1965. EHT calculated results for the dimerization of two ethenes, the prototypical [2+2] cycloaddition. Note the least motion approach of the two ethenes in parallel and overlapping planes. For a ground state reaction, MO13 is the complex for the HOMOs and MO12 is the LUMO (see the numbers at the far left of the column). The energy of each MO is listed for each separation of the two planes containing the ethenes, from 5 Å to 1.55 Å. For more details, see the previous publication in this series on cycloadditions.

Figure 18

Correlation diagrams for the dimerization of two ethenes, the prototypical [2+2] cycloaddition. This figure contains two excerpts from Hoffmann's Laboratory Notebook 16, page 28, ca. February 2, 1965. (Top left) Hoffmann plotted the eHT calculated energies of the HOMO‐2, HOMO‐1, HOMO, LUMO, and LUMO+1, the data from his eHT calculations (reproduced and shown in Figure 22 of the previous publication in this series). (Bottom) Hoffmann then redrew the correlation diagram at top inserting the relevant symmetry elements for the four molecular orbitals and connecting the starting materials with the final product. This is the diagram that appeared in copy‐ready format in the second W−H communication on cycloadditions.

Figure 19

Page 29 from Hoffmann's Laboratory Notebook 16, ca. February 2, 1965. (Top) Hoffmann rederived the correlation diagram for the [4+2] Diels‐Alder cyclization of ethylene and 1,3‐butadiene, thus repeating his correlation diagram for this reaction from page 137 of his Laboratory Notebook 15. Hoffmann's motivation for focusing on the thermal [4+2] cycloaddition at this moment was to compare its mechanism with that of the thermal and photochemical [2+2] cycloadditions on the previous two pages of his laboratory notebook. (Middle) Hoffmann drew the correlation diagram for the boat pathway for the Cope reaction of 1,5‐hexadiene (eq. 1 in Figure 3, where R _i,j =H). (Bottom) Hoffmann mentally drew the correlation diagram for the chair pathway for the Cope reaction of 1,5‐hexadiene and concluded, “same scheme as above.” In the middle, almost certainly written some unknown time later in red ink, he correctly wrote “wrong diagram – see later.” Hoffmann got the MO level crossings in the TS wrong.

Figure 20

Hoffmann's early February 1965 eHT calculations of various conformations of 1,5‐hexadiene on page 32 of his Laboratory Notebook 16. The up and down arrows refer to the relative phases of the MOs.

Figure 21

Page 48 of Roald Hoffmann's Laboratory Notebook 16, ca. February 8, 1965. Hoffmann recorded the total energies and bond orders and energies of the HOMO, HOMO‐1, LUMO, LUMO+1, and LUMO+2 for the complexes consisting of two allyl radicals in parallel planes with atom‐to‐atom overlap approaching each other from 2.0 Å to 5.0 Å; see structure 5 in Figure 4. The arrows for each pair of interacting allyl radicals represent the positive or negative coefficients of the atomic orbitals at each carbon atom, i. e., they provide the phases of each MO. For example, the head of each arrow could represent the positive lobe of a p atomic orbital. Of note, the coordinates of the atoms, these being the input to the eHT calculations, were easy to calculate for this biplanar, symmetrical approach of two allyl radicals.

Figure 22

Page 49 from Hoffmann's Laboratory Notebook 16, ca. February 8, 1965. Hoffmann constructed correlation diagrams for two hypothetical model reactions of a complex consisting of two allyl radicals in either a boat conformation (top) or a chair complex (bottom) yielding either bicyclo[2.2.0]hexane (2) (top) or cyclohexane 1,4‐diyl (3) (bottom), respectively. See also Figure 4 for the two vertical transits therein and displayed in this figure. In these correlation diagrams, the symmetry elements are maintained throughout the reaction, assuming symmetrical reaction pathways. The symmetry elements used by Hoffmann were, for both correlation diagrams, the plane that passes through C(2) and C(5) of the complex; and, for the boat form, a plane parallel to and half‐way between the planes of the approaching allyl radicals; and in the chair, a two‐fold axis of symmetry, perpendicular to the first plane of symmetry.

Figure 23

Page 50 from Hoffmann's Laboratory Notebook 16, ca. February 8, 1965. Hoffmann has constructed correlation diagrams for two hypothetical reactions of (a) complexes consisting of two allyl radicals in either a boat conformation (top) or a chair conformation (bottom), both collapsing to 1,5‐hexadiene (1). There is indeed a symmetry element (plane or two‐fold axis) maintained in this reaction. But it does not help in a general analysis of sigmatropic reactions, i. e., [i,j] when i=j or when i=a hydrogen atom, for which there is no relevant symmetry element. This correlation diagram is essentially a duplicate of what Hoffmann drew on NB16/29 (Figure 19). See also Figure 4.

Figure 24

(A) Page 51 from Hoffmann's Laboratory Notebook 16, ca. February 8, 1965. Hoffmann reconstructed the Cope rearrangement, possibly considering only the boat conformation to the complex consisting of two allyl radicals, as shown below and to the right of the correlation diagram. This is essentially a repeat of what he drew on NB16/29. The symmetry elements in the TS are incorrect. (B) Correlation diagram for the same hypothetical transformation from Hoffmann and Woodward's fifth communication in 1965. This Cope reaction maintains a plane of symmetry for the boat pathway and a C₂ axis of symmetry for the chair pathway. Hence, these symmetry elements are valid during the entire reaction, not just at the symmetrical TS which is the case for [1,j] and [i,j] where i ≠ j sigmatropic reactions.

Figure 25

Excerpt from page 56 from Hoffmann's Laboratory Notebook 16, ca. February 8, 1965. Hoffmann has constructed correlation diagrams for the boat and chair‐like [5,5] reactions. The boat‐like complex proceeds via the hypothetical reaction to the tetracyclic 6 b while the chair‐like complex forms the diradical 6 c. He concluded that the boat‐like mechanism was “very bad Δ [??] hυ“ for the boat and “good Δ” for the chair. In fact, while both are thermally W−H allowed, the chair pathway is the preferred.

Figure 26

Page 70 from Hoffmann's Laboratory Notebook 16, ca. February 10, 1965. On this page, Hoffmann's fascination between the chair and boat conformations of Cope and related rearrangements continued. Here he has constructed interaction diagrams for the chair and boat‐like [3,5] suprafacial‐suprafacial sigmatropic rearrangements and has labelled them according to their symmetry elements, namely, the plane passing through C(3) of the pentadienyl radical (S) and C(2) of the allyl radical (A). He saw a difference between these correlations and those for the [3,3] and [5,5] rearrangements but failed to arrive at any conclusion, at least as written on this page. Of note is the singly occupied MOs (SOMOs) in the nonbonding region of both of correlation diagrams on NB16/70. In each correlation diagram, the SOMOs are of opposite symmetry, A and S, and thus their MOs do not interact and do not lower the energy of a subsequent filled MO had they been of the same symmetry. Hoffmann had not yet recognized that this phenomenon is responsible for the forbidden nature of [3,5] suprafacial sigmatropic rearrangements.

Figure 27

Page 80 from Hoffmann's Laboratory Notebook 16, ca. February 20, 1965. Hoffmann's fascination with the chair and boat conformations of Cope rearrangements continued. Here he has constructed diagrams of two allyl radicals approaching each other in boat‐like and chair‐like complexes to form, ultimately in this hypothetical reaction, the bicyclo[2.2.0]hexane (2) or the diradical, cyclohexane 1,4‐diyl (3), respectively (Figure 4).

Figure 28

(A) In this reaction, the hydrogen moves from C(5) along the top of the plane of the 1,3‐pentadiene molecule to what was originally C(1) with a concomitant shift of the two double bonds. (1) The HOMO overlap interaction method: In the HOMO (the singly‐occupied MO), the phases of the terminal atoms are identical, i. e., both red. In a suprafacial hydrogen migration from C(5) to C(1), the red portion of the orbitals are in‐phase, and the migration is energetically favored. This is a W−H allowed reaction. (2) The interaction diagram/perturbation theory method. The focus of attention is on the TS of this reaction which is modelled by a complex consisting of the 1,3‐pentadienyl radical and a hydrogen atom. The relevant symmetry element is S, the plane of symmetry that is perpendicular to the plane containing the five carbons of the 1,3‐pentadiene molecule and bisects C(3) and the migrating hydrogen atom. On the left of the graphic are sketched a linear representation of the π MOs of 1,3‐pentadienyl radical, showing only the most relevant MOs (proper orbital coefficients are not given). The symmetry of the SOMO of the 1,3‐pentadienyl moiety is S and that for the hydrogen atom is S. Therefore, these two SOMOs mix (or interact), and as shown in the graphic, a stabilized doubly filled MO of lower energy is obtained. The reaction is W−H allowed. The energies/positions for the two SOMOs are not drawn to scale. Compare with Figure 29.

Figure 29

(A) In this reaction, the hydrogen moves from the top side of the plane containing the five carbon atoms of the pentadienyl radical from C(5) to the bottom side of that plane to what was originally C(1) with a concomitant shift of the two double bonds. (1) The HOMO overlap interaction method: In the HOMO (the singly‐occupied MO), the phases of the terminal atoms are opposite, i. e., one is solid red and the other is white with a red outline. In this antarafacial hydrogen migration from C(5) to C(1), the two terminal orbitals are out‐of‐phase, and the migration is energetically disfavored. This is a W−H forbidden reaction. (2) The interaction diagram/perturbation theory method. The focus of attention is on the TS of this reaction which is modelled by a complex consisting of the 1,3‐pentadienyl radical and a hydrogen atom. In the TS, the hydrogen atom is in the plane of the five pentadienyl carbon atoms. The relevant symmetry element is C₂, a two‐fold axis of symmetry. On the left of the graphic is sketched a linear representation of the π MOs of 1,3‐pentadienyl radical, showing only the most relevant MOs (proper orbital coefficients are not given). The symmetry of the SOMO of the 1,3‐pentadienyl moiety is A and that for the hydrogen atom is S. Therefore, the electrons in these two SOMOs remain in the nonbonding region and the energy of the complex is high energy; consequently, the reaction is W−H forbidden. Compare with Figure 28. The energies/positions for the two SOMOs are not to scale.

Figure 30

Page 137 of Hoffmann's Laboratory Notebook 16, ca. March 10, 1965. At the top, Hoffmann wrote, “Woodward has some additional ideas,” and just below that are cycloadditions of ethylene and 1,3‐butadiene with allyl carbocation and two correlation diagrams. Immediately below the cycloadditions are analyses of [1,j] sigmatropic reactions. Hoffmann documented his realization that [1,j] sigmatropic reactions are related to the “1/2 Cope” for a [1,3] migration and to an “extended 1/2 Cope” referring to a [1,5] migration. Below that, Hoffmann drew a [1,7] migration. For these latter three reactions, Hoffmann provided literature references. Two likely interaction diagrams appear in the middle‐right of this page. The upper one “might be a CH minus, to give tetrahedrane as a product.” The lower one is “like cyclopropenyl with benzene. Note the ghostly ring to the left, also the ‘one below two [MO levels] below two below one pattern’.” Their presence on this page is a mystery to Hoffmann and to Seeman; these graphics are unrelated to the cycloadditions above them and to the sigmatropic reactions at the left and below them.

Figure 31

R. B. Woodward, mid‐1960s. Photograph courtesy Brian Salzberg via R. B. Woodward.

Scheme 1

The HOMO overlap interaction method for electrocyclizations. XIII represents the conrotatory W−H allowed thermal ring closure of 1,3‐butadiene with the display of the HOMO of that diene. XIV represents the disrotatory W−H allowed thermal ring closure of 1,3,5‐hexatriene with the display of the HOMO of that triene. Adapted with permission from: Woodward, R. B.; Hoffmann, R. “Stereochemistry of Electrocyclic Reactions.” J. Am. Chem. Soc. 1965, 87, 395–397, 10.1021/ja01080a054. Copyright 1965 American Chemical Society.

Figure 32

HOMO overlap interaction method exemplified by the suprafacial and antarafacial hydrogen migrations in 1,3‐pentadiene. In this method, the symmetries of the SOMOs of the TS fragments are used to determine if the phase of the terminal ends of the fragments are in‐phase (W−H allowed) or out‐of‐phase (W−H forbidden). (B) This graphic shows the MOs of pentadineyl radical, with the HOMO being singly‐occupied, i.e., a SOMO. For the two reactions (A) and (D), the SOMO of the pentadienyl fragment is shown in (B). In (C), the phases match and the [1,5] suprafacial hydrogen migration is W‐H allowed. In (D) and its HOMO overlap interaction diagram (E), the converse obtains, and the [1,5] antarafacial hydrogen migration is W‐H forbidden.

Figure 33

(A) An excerpt from NB16/138, ca. March 10, 1965. In the small graphic at the top line, far right, Hoffmann illustrated the first example of an antarafacial sigmatropic reaction. In the original, the text “all wrong” is in red font, the rest in black font, suggesting that that phrase was added later (and incorrectly so). At the left in the second row are three sets of MO energy levels for the sigmatropic rearrangements shown directly above, with symmetries specified as “S” or “A.” Note the very faint lines at the right edges of the SOMOs of the pentadienyl radical the middle column) in the nonbonding region. These lines refer to the result of mixing or interactions of these two SOMOs having the same symmetry (“S”) to produce two new MOs. One faint line is from the higher energy SOMO that has resulted in a new MO that has gone up in energy, the other faint line indicates the new (and now doubly‐occupied) MO that has gone down in energy. In the first and third columns, the SOMOs have different symmetries and thus do not mix. They remain as high energy nonbonding SOMOs, i. e., radicals. (B) Blow‐up with slight ‘editorial cleaning’ of the upper right‐hand corner of this page. This is an unambiguous illustration of an antarafacial migration of a hydrogen atom from the bottom of the right terminus to the top of the left terminus. “C2 ≠” refers to the model TS of a two‐fold axis of symmetry in an antarafacial sigmatropic reaction. (C) An excerpt from NB17/139. Hoffmann pointed out that an antarafacial hydrogen migration is possible in a [1,7] shift, a suprafacial migration is possible in a [1,5] hydrogen shift, and the observation that a [1,3] hydrogen shift wants to be antarafacial (a C2 symmetry element), i. e., W−H allowed, but this reaction is sterically impossible. Hoffmann wrote, “wants C₂ but can't do”

Scheme 2

Inversion of configuration process at a carbon atom (see 7) in a [1,3] suprafacial sigmatropic rearrangement where the “1” component is a migrating chiral carbon atom. Later studied by Berson and Nelson[ ¹⁴⁹ , ¹⁵⁰ ] this transformation was, at that time, the most dramatic and far‐reaching (supportive) test of the Woodward‐Hoffmann rules. More recent studies have suggested other mechanisms for the experimentally‐observed inversion of configuration at the migrating center in the Berson and Nelson compound.[ ¹⁵¹ , ¹⁵² , ¹⁵³ , ¹⁵⁴ , ¹⁵⁵ ] See additional discussion on this topic in Section 7x. It appears that Woodward and Hoffmann's prediction was right for a reason other than orbital symmetry control.

Figure 34

An excerpt from page 140 from Hoffmann's Laboratory Notebook 16, ca.March 12, 1965. At the top left is an FMO analysis of an antarafacial [1,3] hydrogen migration, a very early example of an antarafacial migration. This pathway is the alternative to suprafacial migrations that form the major focus of Hoffmann's analyses up to this point. To its right is Hoffmann's illustration of what would be a suprafacial [1,5] migration. At the bottom right is an early selection rule for thermal and photochemical sigmatropic rearrangements for both suprafacial (σ symmetry element) and antarafacial (C₂ symmetry element) bonding. At the bottom left is Hoffmann's derivation of MO(5) of 1,3,5‐heptatrienyl.

Figure 35

(A) A black and white reproduction of an excerpt from page 141 of Hoffmann's Laboratory Notebook 16, ca.March 12, 1965. Without much detail, Hoffmann constructed the interaction diagrams for, at the left, a [1,3] suprafacial hydrogen transfer and at the right, a [1,5] suprafacial hydrogen transfer. At the bottom right, Hoffmann wrote, “the difference is that orbitals in center are same symmetry and interact “so that lower own is pushed down,” i. e., stabilized. At the bottom left, Hoffmann listed a number of allylic rearrangements that are possible, but he did not distinguish between suprafacial and antarafacial or between thermal and photochemical or between 4n and 4n+2 electron systems. (B) A portion of the graphic in (A) increased in size and in its original color. Hoffmann drew a red circle around the interaction that is stabilized. Note also that the gap between the A over S in (A, left; the “S” is hard to read but is indeed an “S”) is smaller than the S over S gap in (A, right). The larger the gap, the greater the interaction and the greater the stabilization of the lower, now doubly‐occupied MO.

Figure 36

An excerpt from page 150 of Hoffmann's Laboratory Notebook 16, ca. March 18, 1965. On the first “row” and second “row,” respectively, Hoffmann constructed the interaction diagrams for [1,2] and [1,4] suprafacial hydrogen transfer in cations. At the top left, the doubly occupied HOMO interacts with the LUMO of the migrating moiety, both having S symmetry. There is a net stabilizing interaction, indicated by the MO levels bending downward for the HOMO and bending upward for the LUMO. For the [1,4] hydrogen shift (far left, second row), the double occupied HOMO (of butadiene) is A symmetry while the hydrogen is S symmetry. There is no interaction, and Hoffmann drew the line representing the S level longer. He wrote, “doesn't interact much.” At the bottom, Hoffmann considered carbon shifts in more complex bicyclic systems. He already had some knowledge of carbocation rearrangements in organic chemical systems, e. g., his research on the norbornyl and related carbocations in 1964 and early 1965.[ ⁶⁴ , ⁶⁵ , ¹⁵⁷ ]

Figure 37

Page 152 of Hoffmann's Laboratory Notebook 16, March 19, 1965. The top row of correlation diagrams is for the indicated cycloaddition reactions. The bottom set of interaction diagrams is for non‐inverting carbon shifts in suprafacial sigmatropic reactions. From left to right, [1,2], [1,4], and [1,6] shifts. Hoffmann has constructed correlation diagrams for a series of cationic sigmatropic rearrangements. Stabilizations or destabilizations are indicated by the bending of the various MO levels. Two‐electron and six‐electron systems showed stabilization for sigmatropic reactions while four‐electron systems showed destabilization. Does this not begin to sound like a generalized selection rule based on Hückel's rule and aromaticity?

Figure 38

Excerpt from Hoffmann's NB16/150 (from the top‐left of Figure 36). The HOMO of the π system is shown interacting with the p‐orbital of the migrating species. Both have S symmetry (for a plane of symmetry bisecting the TS) and there is interaction and stabilization for this [1,2] suprafacial sigmatropic reaction.

Figure 39

(A) Page 3 of Hoffmann's Laboratory Notebook 17, ca. March 22, 1965. At the very top, Hoffmann recorded Woodward's observation that “the 3,5 case doesn't fit since if we use 1,n argument, we would a bonding and antibonding situation.” Below that, Hoffmann drew the HOMO (actually SOMO) overlap interaction analysis of a [3,5] suprafacial sigmatropic rearrangement. See bottom graphic in (B). This contains both bonding and antibonding interactions, and the TS is high energy, i. e., W−H forbidden. Just below that, Hoffmann drew three cycloadditions and their partial correlation diagrams (each correlation diagram begins with the shown complex of two radicals at close but not yet bonding distance; and ends with the TS leading to the formation of a cyclic diradical compound). Below that appears to be Hoffmann's search for a W−H allowed [3+5] cycloaddition; I read that line as follows: “A two‐fold axis of symmetry does not exist for a suprafacial [3+3] or a [5+5] cycloaddition but does so for a suprafacial‐antarafacial [5+3] cycloaddition.” Hoffmann then wrote, “Interaction looks the same?” Below that, Hoffmann drew the correlation diagram for an antarafacial‐antarafacial [3+3] cycloaddition of two allyl radicals, as in several lines above. (B) At the top is the interaction diagram/perturbation theory analysis of the π MOs of reacting 1,3‐pentadienyl and allyl radicals. The SOMOs are of opposite symmetry (plane of symmetry bisecting both reactants). Consequently, there is no interaction (mixing) of the MOs and the complex remains as a diradical. At the bottom of (B) is the HOMO overlap interaction analysis method for this same reaction. One of the overlap interactions is bonding and the other is antibonding, i. e., a high energy TS. Both analyses show that the [3,5] suprafacial sigmatropic reaction is high energy, i. e., W−H forbidden. Interpretations of this page are based on several video interview and tutorials with Hoffmann.[ ⁹³ , ¹⁶¹ ]

Scheme 3

(A) Blow‐up of an excerpt from the bottom of page 3 of Hoffmann's Laboratory Notebook 17 (Figure 39). On the top row, on the far right, Hoffmann was thinking about an antarafacial‐suprafacial reaction. (B) Seeman's drawings. The graphic at the far left of (B) duplicates the graphic that Hoffmann drew on the top row, far right in (A). Hoffmann's likely meaning is an antarafacial sigmatropic W−H allowed reaction, as shown in the bottom row, first, second and third graphics. The suprafacial‐suprafacial and antarafacial‐antarafacial reactions are W−H forbidden. In the diagram with the red dashes, the phases are not indicated. For the p‐orbitals perpendicular to the plane of the page, the tops are both black and the bottoms are both white (see Figure 39 B). For the p‐orbitals in the plane of the page, the red dashes point to the black portion of that atomic orbital.

Figure 40

(A) Excerpt from page 16 of Hoffmann's Laboratory Notebook 17. Hoffmann was examining [1,2], [1,3], and [1,4] hydrogen shifts in carbocations. Note also Hoffmann's use of the descriptor “dis”. Note that Hoffmann has simply inserted a vinyl group into the ethyl carbocation. (B) Dewar's 1950—1951 graphic[ ¹⁴³ , ¹⁶⁴ ] illustrating π‐complexes formed by the interaction of the d‐electrons of the silver metal forming a “dative molecular bond with the vacant antibonding π‐MO” of the olefin. In a sense, the TS in Hoffmann's model of sigmatropic rearrangements in carbocations is a rediscovery of Dewar's ideas of π‐complexation from the early 1950s. Dewar also examined HOMO‐LUMO interactions in these analyses.

Figure 41

Page 19 from Hoffmann's Laboratory Notebook 17. Hoffmann is examining many sigmatropic rearragements in carbocations using FMO concepts.

Figure 42

(A) Page 26 from Hoffmann's Laboratory Notebook 17, ca. April 3, 1965. Hoffmann used three MO concepts to analyze sigmatropic rearrangements. At the top and middle, he applied a correlation diagram/interaction diagram with perturbation theory. (B) At the bottom left, he was thinking about a σ 3‐center bond, i. e., TS structure 9, and a π 3 center bond, i. e., TS structure 10. Hoffmann used a HOMO overlap interaction analysis to illustrate either a halogen or hydrogen migration or an inversion at carbon during a sigmatropic rearragement. At the bottom right on NB17/26, Hoffmann considered a three‐center bond model incorporating an inversion at the migrating carbon center. While the atomic orbital at the migrating center in the TS looks like a p‐orbital, and it may even have characteristics resembling a p‐orbital, it is actually the symmetrical σ orbital at its inversion point. This concept appeared in Footonte 4 in W−H's communication on sigmatropic reactions, shown in (B). (B) Graphic 8 from Woodward and Hoffmann's third 1965 communication on sigmatropic reactions, is to be compared with the lower right hand corner of (A). (C) These two graphics represent the graphics at the bottom left in (A) below Hoffmann's text “transfer of type”.

Scheme 4

Berson and Nelson's stereospecific antarafacial [1,3] sigmatropic rearrangement occurs with inversion of stereochemistry at the migrating carbon center, an ingenious experiment in 1967.[ ¹⁴⁹ , ¹⁵⁰ ] This result was consistent with a W−H allowed reaction and was, at that time, the most significant and evidential supporting test of the W−H selection rules. Modern computational chemistry has suggested that the underlying reason for this fascinating stereochemical result – the right result for the wrong reasons – is due to reaction dynamics.[ ¹⁵¹ , ¹⁵² , ¹⁵³ , ¹⁵⁴ ]

Scheme 5

The close relationship between the three‐center bonds present in diborane and the MOs of the allyl fragment. Electron occupation in these MOs is intentionally omitted.

Figure 43

Two methods are used in the analysis of a [1,7] suprafacial hydrogen shift (eq. 10s) at its TS. In 13 and 14, the heavy dots refer to the terminal ends of each fragment. In the linearized MOs just below the structures, the dots refer to the nodes. (A) The reaction under consideration. (B) In the interaction diagram/perturbation theory method, the atoms are broken into two fragments: a hydrogen atom and a 1,3,5‐heptatrienyl radical. (B) In the three‐center bond method, the atoms are broken into two fragments: a pentadienyl radical and a three enter bond, either 15 for a migrating hydrogen atom or 16 for a migrating, inverting carbon atom and its attendant substituents. The sp³ orbitals in 15 and 16 refer to the bonds between the terminal carbon atoms and the migrating group. The placement of the MOs is not to scale. As there is no interaction between the two SOMOs, the complex remains a diradical, and the reaction is high energy, i. e., W−H forbidden.

Figure 44

Two methods are used in the analysis of a [1,7] antarafacial hydrogen shift (eq. 10a) at its TS. In 19 and 20, the heavy dots refer to the terminal ends of each fragment, and this includes the bold H in 19. In the linearized MOs just below the structures, the dots refer to the nodes. (A) The reaction under consideration. (B) In this interaction diagram/perturbation method, the atoms are broken into two fragments: a hydrogen atom and a 1,3,5‐heptatrienyl radical. (C) In a three‐center bond analysis, the atoms are broken into two fragments: a pentadienyl radical and a three enter bond, involving either a hydrogen atom as in 15 or 16 for a migrating carbon atom and its attendant substituents. The SOMOs are analyzed using a two‐fold axis of symmetry that lies in the plane of the three atoms that make up the three‐center bond and bisects <C_αHC_β. For both (B) and (C), the symmetries of the nonbonding electrons in the two SOMOs are identical, i. e., both S in (B) and both A in (C). Consequently, these SOMOs can mix, and a stabilizing interaction occurs with the formation of a new, doubly‐occupied MO that resides in the bonding region, i. e., much lower energy MO than the energies of the two SOMOs (pre‐interaction). This is a W−H allowed reaction. The placement of the MOs is not to scale.

Figure 45

Page 27 of Hoffmann's Laboratory Notebook 17 ca. April 7, 1965, in which Hoffmann derives correlation diagrams of an acyclic and a cyclic sigmatropic rearrangement. In the middle of this page, Hoffmann presented a simple selection rule for thermal and photochemical [1,j] sigmatropic rearrangements.

Figure 46

On NB17/28, Hoffmann discussed suprafacial hydrogen shifts in cyclic systems. The row identifiers (A) – (E) were added by Seeman. Hoffmann used interaction diagrams/perturbation theory and three‐center bonds to explore the qualitative energetics of hydrogen shifts in cyclic systems. The second and third columns in row C are the interaction diagrams for [1,2] and [1,3] migrations in row A. Row D includes three interaction diagrams for the [1.,2], [1,3], and [1,5] hydrogen migrations at the top of row D. The subscripts “3,’ “all,” and “= –” represent various fragments in the above interaction diagrams. Hoffmann also wrote, “so 1,3 hυ expected” and “so 1,5 Δ”. These conclusions are consistent with W−H selection rules, where [1,3] and [1,5] suprafacial migrations are W−H allowed under photochemical and thermal reaction conditions, respectively. Row E (provided by Seeman) corresponds to the fragments in row D and illustrates more clearly the dissection of the TS into the specified MO fragments, for use in the interaction diagrams shown in this figure. In each of the cases in row E, the three‐center bonds are shown with the lines (or curved lines) to and from the hydrogen atom.

Figure 47

Excerpt from page 29 in Hoffmann's Laboratory Notebook 17. Hoffmann used interaction diagrams, three‐center bonds, and qualitative perturbation theory to explore hydrogen shifts in acyclic systems. The subscripts “3” in, for example, A₃, indicates that those MOs refer to the three‐center bond fragment. “al” refers to allyl fragment; “pent” refers to pentadienyl fragment; “H” refers to a hydrogen atom. (Top left) Correlation diagram for suprafacial [1,3] hydrogen shift. The nonbonded electrons in the TS remain at high energy, therefore a W−H disfavored reaction. (Top right) In the first column, Hoffmann drew the MO energy levels of 1,3‐pentadiene followed by two interaction diagrams for the suprafacial [1,5] hydrogen shift. In the penultimate column at top right, Hoffmann drew a three‐center bond fragment (see Figure 42C, structure 9) interacting with an allyl radical. The two SOMOs have the same A symmetry, they interact, there is stabilization (indicated by the down and up arrows and the formation of two new MOs which are not shown), and the reaction is W−H allowed. In the far‐right column, Hoffmann drew the standard interaction diagram for a [1,5] suprafacial migration: an s orbital for the migrating hydrogen and a pentadienyl radical. In the TS, the symmetries of both are S, they interact, a new lower energy doubly‐occupied MO is formed, there is stabilization, and the reaction is W−H allowed! This is, as it should be, the same result as in the penultimate column, W−H allowed. (Bottom) Hoffmann drew two interaction diagrams for an antarafacial [1,7] hydrogen migration. We know that Hoffmann was considering an antarafacial migration for several reasons: the easiest to see is the symmetry assigned by Hoffmann for the lowest doubly‐filled MO of the heptadienyl fragment, namely A; this MO has no nodes, therefore only a C₂ rotation would give an A symmetry. Just as in the case of the suprafacial [1,5] reaction, in the antarafacial [1,7] migration, the two SOMOs in the three‐center bond analysis have the same symmetry (A) and in the heptadienyl fragment/hydrogen radical, the SOMOs again have the same symmetry (S) – consistent with a W−H allowed reaction. It is critical to notice that the interaction diagram/perturbation theory method analyses were performed at the symmetrical TS for all reactions.

Figure 48

(Top) The last two columns of the top row of NB17/29 (Figure 47), for the [1,5] suprafacial sigmatropic reaction of 1,3‐pentadiene. At the left is a three‐center bond analysis, and at the right is the standard pentadienyl – hydrogen atom interaction. (Bottom) A more detailed set of interaction diagrams that relate to Hoffmann's analyses that are directly above. The relative energies of the MOs are not drawn to scale. Hoffmann wrote “funny” (at the bottom of the right column) to describe what seemed odd to him at the time, that the three‐center bond approach has an A—A interaction what is stabilizing while the normal one‐bond approach has an S—S interaction that is also stabilizing. Of course, this is related to the normal alternations in relative phases in the end atomic orbitals as one goes up or down by one level in the MOs of linear polyenes. Analyses performed at the TS.

Figure 49

Page 30 in Hoffmann's Laboratory Notebook 17. Hoffmann used interaction diagrams and three‐center bonds to explore hydrogen shifts and carbanion shifts. He wrote, “preferences reversed in anions.” His thinking is indicated in these diagrams. At the bottom of each column in the top row, Hoffmann wrote a σ (for a plane of symmetry, suprafacial migration) or C₂ (for a two‐fold axis of symmetry (antarafacial migration). To the right of each symmetry designation, he indicated wither the migrating group was a hydrogen atom (no subscript) or the three‐center moiety (subscript “3”). A set of two arrows, up and down, in the vicinity of the nonbonding region indicates MO orbital mixing, delocalization, and stability, i. e., W−H allowed.

Figure 50

Page 34 in Hoffmann's Laboratory Notebook 17, ca. April 9, 1965. At the top, Hoffmann performed eHT calculations on a presumed TS for [1,3] hydrogen shifts, with the hydrogen atom symmetrically located above the allyl radical as shown. Below are Hoffmann's calculations of a [1,5] hydrogen shift. His geometric thinking was written at the very bottom of this page.

Figure 51

Howard E. Zimmerman, University of Wisconsin, mid‐1960s. Photograph courtesy Steven C. Zimmerman.

Figure 52

Two excerpts from Zimmerman and Zweig's 1961 paper. Left, chemical pictograph of XXII–D to XXIII–D (the TS or intermediate in the [1,2] sigmatropic reaction). Right, molecular orbital correlation diagram of XXII–D to XXIII–D. The dots represent one electron, the asterisks represent N electrons (zero, one or two), and the energies listed are in |beta| units. This graphic, very close to a correlation diagram, suggests migration with inversion at the ipso carbon of the migrating phenyl. Symmetries of the MOs were not provided. Only the basis sets are shown. Reprinted with permission from H. E. Zimmerman, A. Zweig, J. Am. Chem. Soc. 1961, 83, 1196‐1213.. Copyright 1961 American Chemical Society.

Figure 53

Page 55 in Hoffmann's Laboratory Notebook 17, ca. April 20, 1965, just about 10 days before the submission of W−H's third communication on sigmatropic reactions. Hoffmann was analyzing and reproducing Zimmerman and Zweig's chemistry shown in Figure 52.

Figure 54

A comparison of the HOMO overlap interaction method (left column) and the interaction diagram/perturbation theory method (right column) for the [1,5] sigmatropic suprafacial and antarafacial reactions. Only occupied MOs of the pentadienyl fragment and the singly‐filled MO of the hydrogen atom are shown. At the top is the suprafacial migration; at the bottom is the antarafacial migration. The migrating hydrogen is shown as a migrating circle; its intended location after the migration is indicated by the dashed unfilled circle. The interaction diagram/perturbation theory method provides the theoretical underpinning for the HOMO overlap interaction method.

Figure 55

Excerpt from the last page of Woodward's second draft of the sigmatropic reaction manuscript. Of note is that Woodward placed his name first, even with the knowledge of the asymmetry in the intellectual contributions made by he and Hoffmann in this research. In the 1960s, the senior author was always listed first.

Figure 56

Excerpts from Hoffmann's and Woodward's drafts of the sigmatropic communication along with the final publication statement dealing with the definition of “sigmatropic reaction. (A) From Hoffmann's first draft. (B) From Hoffmann's second draft. (C) From Hoffmann's third draft. (D) From Woodward's first draft. (E) From Woodward's second draft. (F) From Woodward's third draft. (G) From Woodward and Hoffmann's third communication of 1965 on sigmatropic reactions. The “1” is missing from “j‐1” in the definition.

Figure 57

Excerpt from Woodward's first draft of the sigmatropic communication.

Figure 58

(A) and (B) Woodward's undated handwritten notes, ca. March or April 1965. (A) In this graphic, “sys” and “dia” come from the Greek meaning “the same” and “across,” respectively. Note the suffix of the first three trial terms, “tropic” which perhaps stems from the Ancient Greek, “of or pertaining to a turn or change in type or position.” Note Woodward's term “catastrophic” which he equated with “disrotatory downwards,” and is thus drawing an analogy with electrocyclizations. (B) In this graphic, note the novel terms “similifacial” (“the same”) and “variofacial” (“variety” or “difference”) (middle right). The use of these two terms in Woodward's first draft of the sigmatatropic reaction manuscript suggests that these notes were composed prior to and were used by Woodward in his preparation of his first draft. The chemical reaction at the very bottom of this graphic appeared in the first paragraph of the W−H communication on sigmatropic reactions. (C) Excerpt from the W−H communication on sigmatropic reactions, to be compared with the last line in (B). See the text for a discussion of the other contents of this figure.

Figure 59

(A) Theoretical treatment of sigmatropic reactions in Hoffmann's first draft. This was exclusively a HOMO overlap interaction method. (B) From Woodward and Hoffmann's third 1965 JACS communication on sigmatropic reactions.

Figure 60

In his second draft, Hoffmann provided (A) a three‐center bond explanation in the body of his manuscript and (B) a HOMO overlap interaction explication as a footnote. (C) Woodward and Hoffmann's three‐center bond explanation for a sigmatropic reaction from their 1969 treatise.[ ³ , ⁴ ] Compare with (A). Hoffmann's eventually unused explanation in this draft was more explanatory that that found in their monograph.

Figure 61

Hoffmann's third draft was now typewritten and must be considered a more finished version. (A) Hoffmann continued to feature a three‐center bond explanation in the body of his manuscript and (B) a HOMO overlap interaction explication as footnote 8 in the manuscript. Interesting, footnote 7 was to William Lipscomb's recently published monograph which essentially contained a reproduction of Hoffmann's Ph.D. thesis.

Figure 62

Excerpts from Woodward's first draft of the sigmatropic manuscript. (A) Page 4 shows Woodward's HOMO overlap interaction explanation. Note that the phase of the last atomic orbital is (top) plus over minus and (bottom) minus over plus. (B) Footnote 2 is Woodward's rather lengthy, detailed three‐center bond explanation. Note the rather detailed graphic within this footnote.

Figure 63

Excerpt from Woodward's second draft. The text is identical to what appeared in the third W−H publication (Figure 59B). Note that the phase of the last atomic orbital is (top) plus over minus and (bottom) minus over plus whereas in the third W−H publication, the phase of the last atomic orbital is not provided.

Figure 64

(A) An excerpt from Hoffmann's third draft. (B) An excerpt in Woodward's handwriting from an otherwise typewritten fourth draft of the sigmatropic reaction manuscript. (C) An excerpt from Woodward and Hoffmann's third communication of sigmatropic reactions.

Figure 65

Excerpts dealing with the sigmatropic reaction selection rule from Hoffmann's and Woodward's writings for the sigmatropic manuscript (W−H 3). (A) From Hoffmann's second draft.. The same table appeared in Hoffmann's third draft, a typewritten draft likely provided to Woodward. (B) From Woodward's first draft. (C) From Woodward's second draft. (D) From Woodward and Hoffmann's sigmatropic reaction 1965 communication (W−H 3).

Figure 66

(A) The first page of Hoffmann's second draft of their 1965 JACS communication on sigmatropic reactions (W−H 3). (B) Page 5 of Woodward's third draft of this communication. References , are in Hoffmann's hand. The other handwritten text is by Woodward.

Figure 67

Short note written by Hoffmann to Woodward, ca. March or April 1965.

Figure 68

Excerpt from Woodward's third draft of W−H's third communication which cited Zimmerman's above cited publication. This insert was ultimately not used in the final publication.

Figure 69

(A) Woodward's cover letter to Marshall Gates, then editor in chief of JACS. (B) Marshall Gates's postal card acceptance sent to Woodward on May 3, 1965. This was the standard mode of delivering an acceptance by many ACS journals in the 1960s. “COMM ED” refers to a communication to the editor.

Figure 70

(Top) Thermal [1,7] antarafacial hydrogen migration in the conversion of pre‐vitamin D to vitamin D. (Bottom) Excerpt from Havinga and Schlatmann's 1961 paper depicting the transition state for the pre‐vitamin D$\stackrel{\rightharpoonup }{\leftharpoondown }$ vitamin D interconversions, four years later characterized as an antarafacial [1,7] sigmatropic rearrangement by Woodward and Hoffmann. Reprinted from E. Havinga, J. L. M. A. Schlatmann, Tetrahedron 1961, 16, 146–152. Copyright 1961, with permission from Elsevier.