Determining the N-Representability of a Reduced Density Matrix via Unitary Evolution and Stochastic Sampling

Abstract

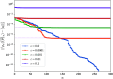
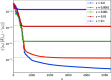
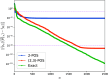
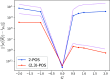
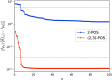
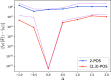
The N-representability problem consists in determining whether, for a given p-body matrix, there exists at least one N-body density matrix from which the p-body matrix can be obtained by contraction, that is, if the given matrix is a p-body reduced density matrix (p-RDM). The knowledge of all necessary and sufficient conditions for a p-body matrix to be N-representable allows the constrained minimization of a many-body Hamiltonian expectation value with respect to the p-body density matrix and, thus, the determination of its exact ground state. However, the number of constraints that complete the N-representability conditions grows exponentially with system size, and hence, the procedure quickly becomes intractable for practical applications. This work introduces a hybrid quantum-stochastic algorithm to effectively replace the N-representability conditions. The algorithm consists of applying to an initial N-body density matrix a sequence of unitary evolution operators constructed from a stochastic process that successively approaches the reduced state of the density matrix on a p-body subsystem, represented by a p-RDM, to a target p-body matrix, potentially a p-RDM. The generators of the evolution operators follow the well-known adaptive derivative-assembled pseudo-Trotter method (ADAPT), while the stochastic component is implemented by using a simulated annealing process. The resulting algorithm is independent of any underlying Hamiltonian, and it can be used to decide whether a given p-body matrix is N-representable, establishing a criterion to determine its quality and correcting it. We apply the proposed hybrid ADAPT algorithm to alleged reduced density matrices from a quantum chemistry electronic Hamiltonian, from the reduced Bardeen-Cooper-Schrieffer model with constant pairing, and from the Heisenberg XXZ spin model. In all cases, the proposed method behaves as expected for 1-RDMs and 2-RDMs, evolving the initial matrices toward different targets.

Figure 1

ADAPT-VQA flowchart.

Figure 2

Distance between the one-body reduced density matrix ¹ρ({θ⃗}) and a fixed noisy target ¹ρ_t as a function of iteration number n for the linear H₄ molecule. The target is constructed by adding random noise of strength ε to the exact ground-state ¹ρ_exact. Distances between the exact (unperturbed) ground-state one-body reduced density matrix and the fixed targets ¹ρ_t are shown as upper-bound references with pink dotted lines. The initial ρ₀ is constructed from the Hartree–Fock ground state.

Figure 3

Distance between the one-body reduced density matrix ¹ρ({θ⃗}) and a fixed noisy target ¹ρ_t as a function of iteration number n for the linear H₄ molecule. The target is constructed by adding random noise of strength ε to the exact first excited state ¹ρ_exact. Distances between the exact (unperturbed) first-excited-state one-body reduced density matrix and the fixed targets ¹ρ_t are shown as upper-bound references with pink dotted lines. The initial ρ₀ is constructed from the Hartree–Fock ground state.

Figure 4

Distance between the two-body reduced density matrix ²ρ({θ⃗}) and a fixed noisy target ²ρ_t as a function of iteration number n for the linear H₄ molecule. The target is constructed by adding random noise of strength ε to the exact ground-state ²ρ_exact. Distances between the exact (unperturbed) ground-state two-body reduced density matrix and the fixed targets ²ρ_t are shown as upper-bound references with pink dotted lines. The initial ρ₀ is constructed from the Hartree–Fock ground state.

Figure 5

Distance between the two-body reduced density matrix ²ρ({θ⃗}) in the reduced BCS model (see text) and three different targets obtained from the v2RDM methods with 2-POS and (2,3)-POS conditions and the exact ground-state solution. Distances between the exact ground-state two-body reduced density matrix and the fixed targets ²ρ_t are shown as upper-bound references with pink dotted lines. The initial ρ₀ is constructed from the mean-field G = 0 pairing model ground state.

Figure 6

Distance between the fully evolved two-body reduced density matrix obtained with the ADAPT-VQA and a fixed target calculated from the 2-POS and (2,3)-POS v2RDM methods for the reduced BCS model. Distances between the exact ground-state two-body reduced density matrix and the fixed targets ²ρ_t are shown as upper-bound references with pink dotted lines. The initial ρ₀ is constructed from the mean-field G = 0 pairing model ground state.

Figure 7

Distance between the two-body reduced density matrix ²ρ({θ⃗}) in the XXZ spin model with anisotropy Δ = 2 (see text) and two target matrices obtained from the v2RDM methods with 2-POS and (2,3)-POS conditions. Distances between the exact ground-state two-body reduced density matrix and the fixed targets ²ρ_t are shown as upper-bound references with pink dotted lines. The initial ρ₀ is chosen as the exact ground state of the Δ = ∞ XXZ model.

Figure 8

Distance between the fully evolved two-body reduced density matrices obtained with the ADAPT-VQA and fixed targets calculated from the v2RDM methods using 2-POS and (2,3)-POS conditions of the XXZ spin model as a function of the anisotropy Δ. The targets are the two-body reduced density matrices computed variationally with two-positivity (2-POS) and partial three-positivity ((2,3)-POS) conditions. Distances between the exact ground-state two-body reduced density matrix and the fixed targets ²ρ_t are shown as upper-bound references with pink dotted lines.