Single-cell imaging of the Mycobacterium tuberculosis cell cycle reveals linear and heterogenous growth
- PMID: 39548343
- PMCID: PMC11602732
- DOI: 10.1038/s41564-024-01846-z
Single-cell imaging of the Mycobacterium tuberculosis cell cycle reveals linear and heterogenous growth
Abstract
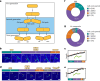
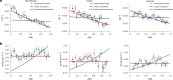
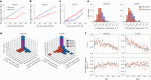
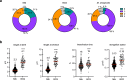
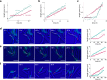
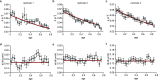
Difficulties in antibiotic treatment of Mycobacterium tuberculosis (Mtb) are partly thought to be due to heterogeneity in growth. Although the ability of bacterial pathogens to regulate growth is crucial to control homeostasis, virulence and drug responses, single-cell growth and cell cycle behaviours of Mtb are poorly characterized. Here we use time-lapse, single-cell imaging of Mtb coupled with mathematical modelling to observe asymmetric growth and heterogeneity in cell size, interdivision time and elongation speed. We find that, contrary to Mycobacterium smegmatis, Mtb initiates cell growth not only from the old pole but also from new poles or both poles. Whereas most organisms grow exponentially at the single-cell level, Mtb has a linear growth mode. Our data show that the growth behaviour of Mtb diverges from that of model bacteria, provide details into how Mtb grows and creates heterogeneity and suggest that growth regulation may also diverge from that in other bacteria.
© 2024. The Author(s).
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures



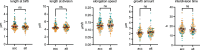
Update of
-
Mycobacterium tuberculosis grows linearly at the single-cell level with larger variability than model organisms.bioRxiv [Preprint]. 2023 May 17:2023.05.17.541183. doi: 10.1101/2023.05.17.541183. bioRxiv. 2023. Update in: Nat Microbiol. 2024 Dec;9(12):3332-3344. doi: 10.1038/s41564-024-01846-z. PMID: 37292927 Free PMC article. Updated. Preprint.
References
-
- Mitchison, D. A. Role of individual drugs in the chemotherapy of tuberculosis. Int. J. Tuberc. Lung Dis.4, 796–806 (2000). - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

