Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Nov 17;14(1):28383.
doi: 10.1038/s41598-024-79102-x.

Solitary wave solutions and sensitivity analysis to the space-time β-fractional Pochhammer-Chree equation in elastic medium

Jan Muhammad  1 , Usman Younas  1 , Ejaz Hussain  2 , Qasim Ali  3 , Mirwais Sediqmal  4 , Krzysztof Kedzia  5 , Ahmed Zubair Jan  5
Affiliations

Solitary wave solutions and sensitivity analysis to the space-time β-fractional Pochhammer-Chree equation in elastic medium

Jan Muhammad et al. Sci Rep. .

Abstract

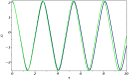
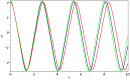
Solitary wave solutions to the nonlinear evolution equations have recently attracted widespread interest in engineering and physical sciences. In this work, we investigate the fractional generalised nonlinear Pochhammer-Chree equation under the power-law of nonlinearity with order m. This equation is used to describe longitudinal deformation wave propagation in an elastic rod. In this study, we have secured a variety of exact solitary wave solutions by the assistance of the recently developed technique known as modified generalized exponential rational function method. Exact solutions of various categories, such as bright-dark, bright, mixed, singular, dark, complex, and combined solitons, are extracted. The applied approach is highly efficient and has a significant computational capability to efficiently tackle the solutions with a high degree of accuracy in nonlinear systems. To analyze the governing system, the equation under investigation is converted to an ordinary differential equation through the application of a suitable wave transformation with a β-derivative. In addition to illustrate the behavior of the solution at various parameter values, we generate 2D and 3D graphs that incorporate pertinent parameters. Moreover, the Galilean transformation is employed to investigate the sensitivity analysis. This research's results have the potential to enhance comprehension of the nonlinear dynamic characteristics displayed by the defined system and to verify the efficacy of the strategies that have been implemented. The results obtained are a substantial contribution to the comprehension of nonlinear science and nonlinear wave fields that are associated with higher dimensions.

Keywords: β-fractional derivative; Generalised nonlinear Pochhammer–Chree equation; Modified generalized exponential rational function method; Power-law nonlinearity; Solitons.

PubMed Disclaimer

Conflict of interest statement

Declarations Competing interest The authors declare no competing interests.

Figures

Fig. 1
Fig. 1
Plots of Eq. (19) for formula image.
Fig. 2
Fig. 2
Plots of Eq. (20) for formula image.
Fig. 3
Fig. 3
Plots of Eq. (29) for formula image.
Fig. 4
Fig. 4
Plots of Eq. (30) for formula image.
Fig. 5
Fig. 5
Sensitivity analysis of system (38) with initial conditions formula image in red (solid line) and formula image in navy blue (solid line).
Fig. 6
Fig. 6
Sensitivity analysis of system (38) with initial conditions formula image in red and formula image in green.
Fig. 7
Fig. 7
Sensitivity analysis of system (38) with initial conditions formula image in navy blue (solid line) and formula image in green (solid line).
Fig. 8
Fig. 8
Sensitivity analysis of system (38) with initial conditions. Three solutions, red, navy blue, and green, indicated by formula image, formula image and, formula image respectively.
See this image and copyright information in PMC

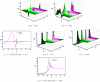
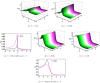
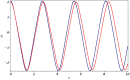
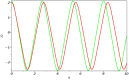
References

    1. Bonnemain, T., Doyon, B. & El, G. Generalized hydrodynamics of the KdV soliton gas. J. Phys. A: Math. Theor.55(37), 374004 (2022).
    1. Petrila, T. & Trif, D. Basics of Fluid Mechanics and Introduction to Computational Fluid Dynamics (Springer Science & Business Media, 2004).
    1. Bykov, V. G. Nonlinear waves and solitons in models of fault block geological media. Russ. Geol. Geophys.56(5), 793–803 (2015).
    1. Ozisik, M. & Akbarov, S. D. Rayleigh-wave propagation in a half-plane covered with a prestressed layer under complete and incomplete interfacial contact. Mech. Compos. Mater.39, 177–82 (2003).
    1. Hereman, W. Shallow water waves and solitary waves. In Solitons pp. 203–220 (Springer US, 2022).

LinkOut - more resources