Statistical Inference for Counting Processes Under Shape Heterogeneity
- PMID: 39562008
- PMCID: PMC12045460
- DOI: 10.1002/sim.10280
Statistical Inference for Counting Processes Under Shape Heterogeneity
Abstract
Proportional rate models are among the most popular methods for analyzing recurrent event data. Although providing a straightforward rate-ratio interpretation of covariate effects, the proportional rate assumption implies that covariates do not modify the shape of the rate function. When the proportionality assumption fails to hold, we propose to characterize covariate effects on the rate function through two types of parameters: the shape parameters and the size parameters. The former allows the covariates to flexibly affect the shape of the rate function, and the latter retains the interpretability of covariate effects on the magnitude of the rate function. To overcome the challenges in simultaneously estimating the two sets of parameters, we propose a conditional pseudolikelihood approach to eliminate the size parameters in shape estimation, followed by an event count projection approach for size estimation. The proposed estimators are asymptotically normal with a root- convergence rate. Simulation studies and an analysis of recurrent hospitalizations using SEER-Medicare data are conducted to illustrate the proposed methods.
Keywords: dimension reduction; kernel smoothing; recurrent event process; single index model.
© 2024 John Wiley & Sons Ltd.
Conflict of interest statement
Conflicts of Interest
The authors declare no conflicts of interest.
Figures
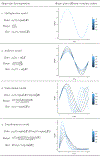
References
-
- Lawless JF and Nadeau C, “Some Simple Robust Methods for the Analysis of Recurrent Events,” Technometrics 37, no. 2 (1995): 158–168.
-
- Lin DY, Wei LJ, Yang I, and Ying Z, “Semiparametric Regression for the Mean and Rate Functions of Recurrent Events,” Journal of the Royal Statistical Society: Series B 62, no. 4 (2000): 711–730.
-
- Gail M, Santner T, and Brown C, “An Analysis of Comparative Carcinogenesis Experiments Based on Multiple Times to Tumor,” Biometrics 36 (1980): 255–266. - PubMed
-
- Prentice RL, Williams BJ, and Peterson AV, “On the Regression Analysis of Multivariate Failure Time Data,” Biometrika 68, no. 2 (1981): 373–379.
-
- Andersen PK and Gill RD, “Cox’s Regression Model for Counting Processes: A Large Sample Study,” Annals of Statistics 10 (1982): 1100–1120.
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
