Private detection of relatives in forensic genomics using homomorphic encryption

Abstract

Background: Forensic analysis heavily relies on DNA analysis techniques, notably autosomal Single Nucleotide Polymorphisms (SNPs), to expedite the identification of unknown suspects through genomic database searches. However, the uniqueness of an individual's genome sequence designates it as Personal Identifiable Information (PII), subjecting it to stringent privacy regulations that can impede data access and analysis, as well as restrict the parties allowed to handle the data. Homomorphic Encryption (HE) emerges as a promising solution, enabling the execution of complex functions on encrypted data without the need for decryption. HE not only permits the processing of PII as soon as it is collected and encrypted, such as at a crime scene, but also expands the potential for data processing by multiple entities and artificial intelligence services.

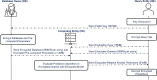
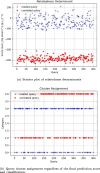
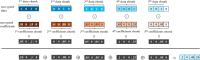
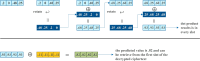
Methods: This study introduces HE-based privacy-preserving methods for SNP DNA analysis, offering a means to compute kinship scores for a set of genome queries while meticulously preserving data privacy. We present three distinct approaches, including one unsupervised and two supervised methods, all of which demonstrated exceptional performance in the iDASH 2023 Track 1 competition.

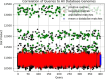
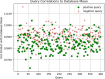
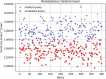
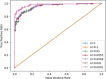
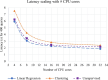
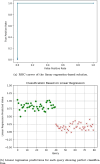
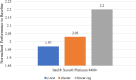
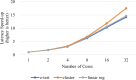
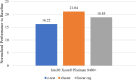
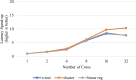
Results: Our HE-based methods can rapidly predict 400 kinship scores from an encrypted database containing 2000 entries within seconds, capitalizing on advanced technologies like Intel AVX vector extensions, Intel HEXL, and Microsoft SEAL HE libraries. Crucially, all three methods achieve remarkable accuracy levels (ranging from 96% to 100%), as evaluated by the auROC score metric, while maintaining robust 128-bit security. These findings underscore the transformative potential of HE in both safeguarding genomic data privacy and streamlining precise DNA analysis.

Conclusions: Results demonstrate that HE-based solutions can be computationally practical to protect genomic privacy during screening of candidate matches for further genealogy analysis in Forensic Genetic Genealogy (FGG).

Keywords: Data privacy; Genomic database; Homomorphic encryption; Secure query.

Fig. 1

Classic secure outsourcing computing protocol used in the iDASH 2023 Homomorphic Encryption challenge. 400 queries and 2000 database samples make up the bulk of the data movement, each requires 956KB of storage space. The size of encrypted predictions displayed in the picture corresponds to 400 encrypted predictions, i.e. 51MB

Fig. 2

CKKS ciphertext structure depicting the noise budget in a freshly encrypted ciphertext

Fig. 3

This plot shows the correlation value of each query with every sample in the genomic database

Fig. 4

Scatter plot showing the correlation of positive and negative queries with respect to the database mean

Fig. 5

Scatter plot of relatedness determinants per query calculated using Eq. 4. Weighing the distance by the variance allows for better linear decision boundary

Fig. 6

ROC curve plot of the unsupervised solution for different threshold values and different choices of e. Each ROC curve is plotted by varying the threshold with fixed e value

Fig. 7

This figure shows the ciphertext packing that allows SIMD computation

Algorithm 1 Drop the moduli of the ciphertext with more levels to match the ciphertext with less number of levels

Algorithm 2 Computation of the linearly approximated constant fraction $\frac{1}{\sqrt{{\mu }_i+e}}$

Algorithm 3 Computation of the inner sum of the elements in the slots of a vector of ciphertexts, which is described by the last two equations in Eq. 16. N is the polynomial ring size, such that N/2 corresponds to the number of slots. Here we assume empty slots are filled with zeros

Algorithm 4 Fully Unsupervised Algorithm: Z-Test Inspired Method (Eq. 7)

Fig. 8

Summary plots of the clustering-based solution

Algorithm 5 Cluster-Point Correlation Method (Eq. 10)

Fig. 9

Toy illustration of SIMD dot product with CKKS ciphertexts

Fig. 10

Toy illustration of how the Rotation operation helps sum all the elements in the slots of a CKKS ciphertext

Algorithm 6 Linear Regression Method (Eq. 16)

Fig. 11

Illustration of genome sequence data. Genome sequences are organized as columns and their genotypes organized as rows

Fig. 12

Graph showing how all three methods scale latency with increasing availability of CPU cores for inference of 400 queries

Fig. 13

ROC curve of the clustering-based solution

Fig. 14

Linear Regression-based prediction performance: a plot of the ROC curve showing perfect prediction, and b scatter plot of the predicted values for each query showing linearly separable classification decision boundary

Fig. 15

Performance gain due to algorithm choice

Fig. 16

Performance gain due to vector instructions

Fig. 17

Latency with varying number of cores under the third scenario, i.e. multicore execution without the use of vectorized instructions

Fig. 18

Performance gain due to parallel processing with multiple cores alone. The performance gain (normalized performance to baseline) is calculated as the throughput ratio between the execution using multiple cores over single core. The optimal number of cores for all the workloads is 32

Fig. 19

Performance gain due to parallel processing with vectorized instructions and usage of multiple cores together. The performance gain (normalized performance to baseline) is calculated as the throughput ratio between the execution using vectorized instructions plus multiple cores over single core. The optimal number of cores for both z-test and linear reg workloads is 16 due to reaching AVX512 overhead, whereas for the cluster workload is 32, less affected by AVX512 overhead

Fig. 20

Latency with varying number of cores under the fourth scenario, i.e. multicore execution with the use of vector instructions