The TWW Growth Model and Its Application in the Analysis of Quantitative Polymerase Chain Reaction
- PMID: 39568449
- PMCID: PMC11577475
- DOI: 10.1177/11779322241290126
The TWW Growth Model and Its Application in the Analysis of Quantitative Polymerase Chain Reaction
Abstract
It is necessary to accurately capture the growth trajectory of fluorescence where the best fit, precision, and relative efficiency are essential. Having this in mind, a new family of growth functions called TWW (Tabatabai, Wilus, Wallace) was introduced. This model is capable of accurately analyzing quantitative polymerase chain reaction (qPCR). This new family provides a reproducible quantitation of gene copies and is less labor-intensive than current quantitative methods. A new cycle threshold based on TWW that does not need the assumption of equal reaction efficiency was introduced. The performance of TWW was compared with 3 classical models (Gompertz, logistic, and Richard) using qPCR data. TWW models the relationship between the cycle number and fluorescence intensity, outperforming some state-of-the-art models in performance measures. The 3-parameter TWW model had the best model fit in 68.57% of all cases, followed by the Richard model (28.57%) and the logistic (2.86%). Gompertz had the worst fit in 88.57% of all cases. It had the best precision in 85.71% of all cases followed by Richard (14.29%). For all cases, Gompertz had the worst precision. TWW had the best relative efficiency in 54.29% of all cases, while the logistic model was best in 17.14% of all cases. Richard and Gompertz tied for the best relative efficiency in 14.29% of all cases. The results indicate that TWW is a good competitor when considering model fit, precision, and efficiency. The 3-parameter TWW model has fewer parameters when compared to the Richard model in analyzing qPCR data, which makes it less challenging to reach convergence.
Keywords: Cy0 method; Gompertz growth model; Quantitative polymerase chain reaction; cycle threshold; logistic growth model; the Richard growth model.
© The Author(s) 2024.
Conflict of interest statement
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Figures





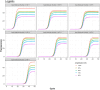
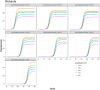

Similar articles
-
qPCR data analysis: Better results through iconoclasm.Biomol Detect Quantif. 2019 Jun 5;17:100084. doi: 10.1016/j.bdq.2019.100084. eCollection 2019 Mar. Biomol Detect Quantif. 2019. PMID: 31194178 Free PMC article.
-
A new real-time PCR method to overcome significant quantitative inaccuracy due to slight amplification inhibition.BMC Bioinformatics. 2008 Jul 30;9:326. doi: 10.1186/1471-2105-9-326. BMC Bioinformatics. 2008. PMID: 18667053 Free PMC article.
-
Antibiotic resistance gene load and irrigation intensity determine the impact of wastewater irrigation on antimicrobial resistance in the soil microbiome.Water Res. 2021 Apr 1;193:116818. doi: 10.1016/j.watres.2021.116818. Epub 2021 Jan 8. Water Res. 2021. PMID: 33571903
-
The use of Gompertz models in growth analyses, and new Gompertz-model approach: An addition to the Unified-Richards family.PLoS One. 2017 Jun 5;12(6):e0178691. doi: 10.1371/journal.pone.0178691. eCollection 2017. PLoS One. 2017. PMID: 28582419 Free PMC article. Review.
-
Comprehensive technological assessment for different treatment methods of leather tannery wastewater.Environ Sci Pollut Res Int. 2023 Dec;30(60):124686-124703. doi: 10.1007/s11356-022-21259-x. Epub 2022 Jun 9. Environ Sci Pollut Res Int. 2023. PMID: 35680745 Review.
References
-
- Ashton Acton Q. Blood Cells-Advances in Research and Application. ScholarlyMedia LLC; 2012.
-
- Wadkin LE, Orozco-Fuentes S, Neganova I, et al.. An introduction to the mathematical modelling of iPSCs. http://arxiv.org/abs/2010.15493 (2020, accessed 7 September 2023).
-
- Allman ES, Rhodes JA. Mathematical Models in Biology: An Introduction. 1st ed. Cambridge University Press; 2003.
Grants and funding
LinkOut - more resources
Full Text Sources

