Using Joint Longitudinal and Time-to-Event Models to Improve the Parameterization of Chronic Disease Microsimulation Models: an Application to Cardiovascular Disease

Abstract

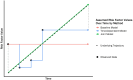
Background: Chronic disease microsimulation models often simulate disease incidence as a function of risk factors that evolve over time (e.g., blood pressure increasing with age) in order to facilitate decision analyses of different disease screening and prevention strategies. Existing models typically rely on incidence rates estimated with standard survival analysis techniques (e.g., proportional hazards from baseline data) that are not designed to be continually updated each model cycle. We introduce the use of joint longitudinal and time-to-event to parameterize microsimulations to avoid potential issues from using these existing methods. These joint models include random effects regressions to estimate the risk factor trajectories and a survival model to predict disease risk based on those estimated trajectories. In a case study on cardiovascular disease (CVD), we compare the validity of microsimulation models parameterized with this joint model approach to those parameterized with the standard approaches.

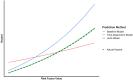
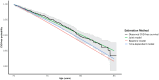
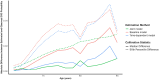
Methods: A CVD microsimulation model was constructed that modeled the trajectory of seven CVD risk factors/predictors as a function of age (smoking, diabetes, systolic blood pressure, antihypertensive medication use, total cholesterol, HDL, and statin use) and predicted yearly CVD incidence as a function of these predictors, plus age, sex, and race. We parameterized the model using data from the Atherosclerosis Risk in Communities study (ARIC). The risk of CVD in the microsimulation was parameterized with three approaches: (1) joint longitudinal and time-to-event model, (2) proportional hazards model estimated using baseline data, and (3) proportional hazards model estimated using time-varying data. We accounted for non-CVD mortality across all the parameterization approaches. We simulated risk factor trajectories and CVD incidence from age 70y to 85y for an external test set comprised of individuals from the Multi-Ethnic Study of Atherosclerosis (MESA). We compared the simulated to observed incidence using both average survival curves and the E50 and E90 calibration metrics (the median and 90th percentile absolute difference between observed and predicted incidence) to measure the validity of each parameterization approach.

Results: The average CVD survival curve estimated by the microsimulation model parameterized with the joint model approach matched the observed curve from the test set relatively closely. The other parameterization methods generally performed worse, especially the proportional hazards model estimated using baseline data. Similar results were observed for the calibration metrics, with the joint model performing particularly well on the E90 metric compared to the other models.

Conclusions: Using a joint longitudinal and time-to-event model to parameterize a CVD simulation model produced incidence predictions that more accurately reflected observed data than a model parameterized with standard approaches. This parameterization approach could lead to more reliable microsimulation models, especially for models that evaluate policies which depend on tracking dynamic risk factors over time. Beyond this single case study, more work is needed to identify the specific circumstances where the joint model approach will outperform existing methods.

Figure 1:

Stylized microsimulation model structure for chronic disease prevention and screening models v_i(t): Vector of risk factors values at time t (e.g., blood pressure, smoking status) for individual i in the model population. p(v_i(t)): Probability of an event (e.g., stroke, heart attack) from time t to t + 1 based on risk factor values

Figure 2:

Assumptions about risk factor values over time by risk estimation method from illustrative example Underlying trajectory (dashed line): The actual risk factor values increase linearly over time but there is measurement error, as shown by the observed data points. Baseline Model (red line): Assumes starting risk factor value stays constant over time, and that values are measured without error. Time-Dependent Model (blue line): Assumes last-observed risk factor value is constant until next observation, and that values are measured without error. Joint Model (green line): Fits random effects regression model to interpolate extrapolate risk factor trajectory, and accounts for random measurement error.

Figure 3:

Estimated hazard by risk estimation method from illustrative example Actual Hazard (dashed line): Increases along with increases in risk factor values. Baseline Model (red line): Attributes future increases in hazard to an underlying time-trend because only lower initial risk factors are used to estimate risk, so the model underestimates the relationship between the risk factor values and event risk. Time-Dependent Model (blue line): Since risk factor value observations stop midway through follow-up, attributes future increases in hazard in second-half of follow-up to lower carried-forward risk factor values. This overestimates the relationship between the risk factor values and event risk. Joint Model (green line): Attributes future increases in hazard to extrapolated increased risk factor values, so the model accurately estimates relationship between risk factor and event risk.

Figure 4:

Average CVD survival curves for microsimulation models with age 70 starting cohort Gray region is 95% confidence interval of observed CVD survival curve calculated with the log-log approach.

Figure 5:

Calibration metrics for microsimulation models with age 70 starting cohort