Frugal inference for control

Abstract

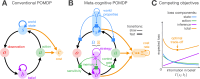
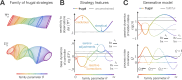
A key challenge in advancing artificial intelligence is achieving the right balance between utility maximization and resource use by both external movement and internal computation. While this trade-off has been studied in fully observable settings, our understanding of resource efficiency in partially observable environments remains limited. Motivated by this challenge, we develop a version of the POMDP framework where the information gained through inference is treated as a resource that must be optimized alongside task performance and motion effort. By solving this problem in environments described by linear-Gaussian dynamics, we uncover fundamental principles of resource efficiency. Our study reveals a phase transition in the inference, switching from a Bayes-optimal approach to one that strategically leaves some uncertainty unresolved. This frugal behavior gives rise to a structured family of equally effective strategies, facilitating adaptation to later objectives and constraints overlooked during the original optimization. We illustrate the applicability of our framework and the generality of the principles we derived using two nonlinear tasks. Overall, this work provides a foundation for a new type of rational computation that both brains and machines could use for effective but resource-efficient control under uncertainty.

Figure 1

Structure of computationally constrained control. A) Conventional POMDP. The agent interacts with a hidden world state over time, receiving noisy observations, taking actions that change the state, and incurring costs based on the action taken and the resulting next state. Minimizing cumulative costs requires managing state uncertainty. To address this, the agent builds and updates a belief over the hidden state that aims to fully summarize previous evidence (the history of past observations and actions). B) Meta-cognitive POMDP. The agent pays for the information that beliefs encode about hidden world states. To balance this internal cost against state and action costs, the agent computes a strategy $\mathrm{Ж}$ that dictates how to integrate new evidence and how to transform the resulting beliefs into actions. To compute this strategy, the agent considers the properties of the world, $\text{Ω}$, and the penalty parameters of the loss function, $\text{Ξ}$; factors that we assume are fully observable and change slowly. C) Optimal trade-off. State and action costs decrease as the belief encodes more information about the hidden state. However, when information is costly, the agent can achieve greater utility by tolerating more state and action costs if doing so saves enough bits in the inference. This research highlights principles that allow optimizing this trade-off in POMDPs with linear-Gaussian dynamics.

Figure 2

Parameter space for frugal inference. A) Phase transition in the optimal inference strategy. The penalties $C_s$ and $C_n$, which determine the relative importance of minimizing state deviations and reducing information use, set a threshold (white line) beyond which the benefits of Bayes-optimal inference saturate. Markers $p_1$ and $p_2$ indicate parameters at which the optimization landscapes of Plots B and C are defined. B) Optimization landscape before the phase transition. The optimization landscape of the planning problem is convex when the agent relies on Bayes-optimal inference. C) Optimization landscape after the phase transition. When the agent leaves some epistemic uncertainty unresolved, the optimization landscape has multiple global minima. The multiple solutions achieve statistically equivalent performance but differ in how the agent integrates new evidence, offsets estimation errors, and generalizes to novel settings.

Figure 3

Family of frugal strategies. A) Graphical representation of optimized strategies. For 2-dimensional control tasks, the solutions are described by 2×2 matrices of observation sensitivity $\text{Ψ}$ and controller’s base dynamics $\text{Π}$. Here these matrices are visualized by how they transform a unit circle into an ellipse. Members of this family of strategies are related by an orthogonal transformation that is fully defined by a free angle $\theta$ (depicted by hue). For each color there is a pair of ellipses for the surfaces of $\text{Ψ}$ and $\text{Π}$, representing a strategic combination of lossy inference and error-aware control. B) Strategy features. The family members differ in how the agent integrates new evidence and offsets estimation errors. For instance, the strategies prioritizing observations over predictions require controllers that frequently change the direction of motion. In contrast, the strategies that prioritize predictions over observations rely on controllers that correct deviations with gradual, smooth movements. The combination of inference and control that solves the unconstrained control problem is shown in gray. C) Generative model. To save bits in the inference, the agent makes deliberately mistaken assumptions about the world. Some strategies model the stochasticity in the transition dynamics as stable oscillations with high process noise (orange-hued members); others explain this randomness as low process noise in a volatile environment (blue-hued members). The ground truth properties are shown in gray.

Figure 4

Trade-off between motion effort and inference cost. The best control gain with costly information is higher than the best control gain when information is free. This additional motion effort serves two purposes, depending on inference quality, as shown here: A) Additional motion when using Bayes-optimal inference. The agent applies a strong control gain to decrease state variance; this approach indirectly lowers inference cost by reducing the variability that previous evidence has to explain. B) Additional motion when using lossy inference. The agent applies a strong control gain to offset the estimation errors arising from unresolved uncertainty.

Figure 5

Frugal control for balancing a pole. A) Schematic of relevant variables. The controller aims to balance the pole on a moving cart by adjusting the cart’s acceleration. B) Inference sensitivity to observations. The unconstrained agent (gray) weighs observations based solely on statistical reliability. In contrast, frugal agents (non-gray) also take control objectives into account. This entails a strategic adjustment of observation weights that, when paired with a suitable control policy, optimizes information usage while still ensuring eventual goal attainment. C) Control trajectories for different agents. Skeptical inference can be compensated by a serene controller that adjusts the cart’s acceleration gradually. However, credulous inference requires a reactive controller that frenetically changes the direction of motion. D) State-space trajectories. Both frugal agents (non-gray trajectories) are able to attain the goal, stabilizing the pole at the upright position. Individual trials are displayed in light colors, with the mean trajectory emphasized in dark. E) Statistical performance at equilibrium. Although the frugal strategies differ noticeably during the transient, they incur statistically identical state, action, and inference costs at equilibrium. Error bars indicate one standard deviation

Figure 6

Frugal control of a planar drone maintaining a fixed hover position. A) Schematic of relevant variables. B) Family of frugal strategies. For a two-dimensional controller, the solution to the planning problem comprises infinite combinations of lossy inference and error-aware control. These strategies differ in how the agent integrates new evidence (top), offsets estimation errors (middle), and generalizes to novel settings (bottom). C) State-space trajectories. The frugal strategies successfully drive the system to an equilibrium near the target state. During the transient, combining skeptical inference with serene control yields state-space trajectories that differ substantially from those generated by an unconstrained agent, a credulous and reactive agent, and a serene agent with oscillations. This behavior is in line with our sensitivity analysis (panel B, bottom), which indicates that combining skeptical inference with serene control is highly sensitive to model mismatch. Here, the mismatch arises because the trajectories reflect the true nonlinear dynamics, whereas the strategies were computed using linearized approximations of those dynamics. Individual trials are displayed in light colors, with the mean trajectory emphasized in dark. D) Statistical performance at equilibrium. All family members perform equally well under linear dynamics (top), but respond differently when evaluated using simulations of the nonlinear model (bottom). Mean cost is shown by lines, with shaded regions denoting one standard deviation; unconstrained performance is marked by a dot on the vertical axis.