Nanocavities for Molecular Optomechanics: Their Fundamental Description and Applications
- PMID: 39584033
- PMCID: PMC11583369
- DOI: 10.1021/acsphotonics.4c01548
Nanocavities for Molecular Optomechanics: Their Fundamental Description and Applications
Abstract
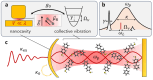
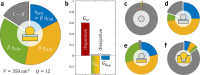
Vibrational Raman scattering-a process where light exchanges energy with a molecular vibration through inelastic scattering-is most fundamentally described in a quantum framework where both light and vibration are quantized. When the Raman scatterer is embedded inside a plasmonic nanocavity, as in some sufficiently controlled implementations of surface-enhanced Raman scattering (SERS), the coupled system realizes an optomechanical cavity where coherent and parametrically amplified light-vibration interaction becomes a resource for vibrational state engineering and nanoscale nonlinear optics. The purpose of this Perspective is to clarify the connection between the languages and parameters used in the fields of molecular cavity optomechanics (McOM) versus its conventional, "macroscopic" counterpart and to summarize the main results achieved so far in McOM and the most pressing experimental and theoretical challenges. We aim to make the theoretical framework of molecular cavity optomechanics practically usable for the SERS and nanoplasmonics community at large. While quality factors (Q) and mode volumes (V) essentially describe the performance of a nanocavity in enhancing light-matter interaction, we point to the light-cavity coupling efficiencies (η) and optomechanical cooperativities () as the key parameters for molecular optomechanics. As an illustration of the significance of these quantities, we investigate the feasibility of observing optomechanically induced transparency with a molecular vibration-a measurement that would allow for a direct estimate of the optomechanical cooperativity.
© 2024 The Authors. Published by American Chemical Society.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
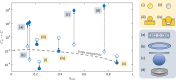
 , while full blue symbols represent
, while full blue symbols represent  . The data for dielectric cavities
are compiled
from published experiments: (a) ref (41), (b) ref (42), (c) ref (43), and (d) ref (44).
. The data for dielectric cavities
are compiled
from published experiments: (a) ref (41), (b) ref (42), (c) ref (43), and (d) ref (44).
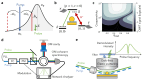
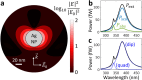
 and external
coupling efficiency ηrad. (d) Possible OMIT measurement
scheme in macroscopic cOM.
Adapted with permission from ref (140). Copyright 2020 American Physical Society.
PLL, phase-locked loop; FC, filter cavity; PM, phase modulator. (e)
Proposed implementation of OMIT measurement in McOM using a dark-field
geometry for pump and probe excitation. A spectral filter blocks the
pump, and the probe signal is sent to the detector. The pump (pulsed
or cw) is intensity-modulated so that the demodulated scattered probe
intensity senses the pump-induced change in cavity scattering, which
can have thermal (broad plasmonic response) or optomechanical (narrow
vibrational response) origins.
and external
coupling efficiency ηrad. (d) Possible OMIT measurement
scheme in macroscopic cOM.
Adapted with permission from ref (140). Copyright 2020 American Physical Society.
PLL, phase-locked loop; FC, filter cavity; PM, phase modulator. (e)
Proposed implementation of OMIT measurement in McOM using a dark-field
geometry for pump and probe excitation. A spectral filter blocks the
pump, and the probe signal is sent to the detector. The pump (pulsed
or cw) is intensity-modulated so that the demodulated scattered probe
intensity senses the pump-induced change in cavity scattering, which
can have thermal (broad plasmonic response) or optomechanical (narrow
vibrational response) origins.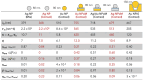
References
-
- Ru E. L.; Etchegoin P.. Principles of Surface-Enhanced Raman Spectroscopy: And Related Plasmonic Effects; Elsevier, 2008.
-
- Aspelmeyer M.; Kippenberg T. J.; Marquardt F. Cavity Optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. 10.1103/RevModPhys.86.1391. - DOI
Publication types
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous
