An inductive bias for slowly changing features in human reinforcement learning
- PMID: 39585903
- PMCID: PMC11637442
- DOI: 10.1371/journal.pcbi.1012568
An inductive bias for slowly changing features in human reinforcement learning
Abstract
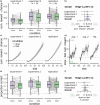
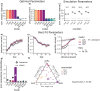
Identifying goal-relevant features in novel environments is a central challenge for efficient behaviour. We asked whether humans address this challenge by relying on prior knowledge about common properties of reward-predicting features. One such property is the rate of change of features, given that behaviourally relevant processes tend to change on a slower timescale than noise. Hence, we asked whether humans are biased to learn more when task-relevant features are slow rather than fast. To test this idea, 295 human participants were asked to learn the rewards of two-dimensional bandits when either a slowly or quickly changing feature of the bandit predicted reward. Across two experiments and one preregistered replication, participants accrued more reward when a bandit's relevant feature changed slowly, and its irrelevant feature quickly, as compared to the opposite. We did not find a difference in the ability to generalise to unseen feature values between conditions. Testing how feature speed could affect learning with a set of four function approximation Kalman filter models revealed that participants had a higher learning rate for the slow feature, and adjusted their learning to both the relevance and the speed of feature changes. The larger the improvement in participants' performance for slow compared to fast bandits, the more strongly they adjusted their learning rates. These results provide evidence that human reinforcement learning favours slower features, suggesting a bias in how humans approach reward learning.
Copyright: © 2024 Hedrich et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures





Similar articles
-
Humans combine value learning and hypothesis testing strategically in multi-dimensional probabilistic reward learning.PLoS Comput Biol. 2022 Nov 23;18(11):e1010699. doi: 10.1371/journal.pcbi.1010699. eCollection 2022 Nov. PLoS Comput Biol. 2022. PMID: 36417419 Free PMC article.
-
Multi-task reinforcement learning in humans.Nat Hum Behav. 2021 Jun;5(6):764-773. doi: 10.1038/s41562-020-01035-y. Epub 2021 Jan 28. Nat Hum Behav. 2021. PMID: 33510391
-
Momentary subjective well-being depends on learning and not reward.Elife. 2020 Nov 17;9:e57977. doi: 10.7554/eLife.57977. Elife. 2020. PMID: 33200989 Free PMC article.
-
A Normative Account of Confirmation Bias During Reinforcement Learning.Neural Comput. 2022 Jan 14;34(2):307-337. doi: 10.1162/neco_a_01455. Neural Comput. 2022. PMID: 34758486 Free PMC article.
-
Exploring Feature Dimensions to Learn a New Policy in an Uninformed Reinforcement Learning Task.Sci Rep. 2017 Dec 15;7(1):17676. doi: 10.1038/s41598-017-17687-2. Sci Rep. 2017. PMID: 29247192 Free PMC article.
References
MeSH terms
LinkOut - more resources
Full Text Sources

