Information Propagation in Hypergraph-Based Social Networks

Abstract

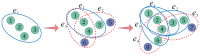
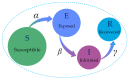
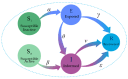
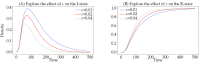
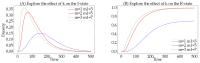
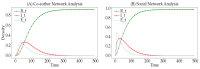
Social networks, functioning as core platforms for modern information dissemination, manifest distinctive user clustering behaviors and state transition mechanisms, thereby presenting new challenges to traditional information propagation models. Based on hypergraph theory, this paper augments the traditional SEIR model by introducing a novel hypernetwork information dissemination SSEIR model specifically designed for online social networks. This model accurately represents complex, multi-user, high-order interactions. It transforms the traditional single susceptible state (S) into active (Sa) and inactive (Si) states. Additionally, it enhances traditional information dissemination mechanisms through reaction process strategies (RP strategies) and formulates refined differential dynamical equations, effectively simulating the dissemination and diffusion processes in online social networks. Employing mean field theory, this paper conducts a comprehensive theoretical derivation of the dissemination mechanisms within the SSEIR model. The effectiveness of the model in various network structures was verified through simulation experiments, and its practicality was further validated by its application on real network datasets. The results show that the SSEIR model excels in data fitting and illustrating the internal mechanisms of information dissemination within hypernetwork structures, further clarifying the dynamic evolutionary patterns of information dissemination in online social hypernetworks. This study not only enriches the theoretical framework of information dissemination but also provides a scientific theoretical foundation for practical applications such as news dissemination, public opinion management, and rumor monitoring in online social networks.

Keywords: hypergraph; information propagation; online social networks; response process strategies.

Figure 1

Evolutionary schematic of the hypernetwork model ($m=2$; $m_1=3$). Blue solid lines indicate existing hyperedges, green nodes denote existing nodes, red dashed lines depict new hyperedges added in the current time step, and blue nodes signify new nodes added during the current time step.

Figure 2

SEIR model state transition diagram. In the context of information dissemination, the green section represents the $S$-state, indicating unawareness of the information. The dark blue section is the $E$-state, where individuals are aware of but not spreading the information. The purple section denotes the $I$-state, where individuals actively spread the information. The light blue section represents the $R$-state, indicating immunity to the information.

Figure 3

SSEIR model state transition diagram. Dark green denotes the $S_i$-state, light green denotes the $S_a$-state, dark blue denotes the $E$-state, purple denotes the $I$-state, and light blue denotes the $R$-state.

Figure 4

Comparison chart of theoretical and simulation trends in information dissemination. The green dashed line represents theoretical values for the $R$-state, the red dashed line for the $I$-state, and the light blue dashed line for the $E$-state. Green star-shaped markers denote simulation results for the $R$-state, red stars for the $I$-state, and light blue stars for the $E$-state.

Figure 5

Trends of information dissemination across different network models. Deep blue denotes the $S_i$-state, black denotes the $S_a$-state, light blue denotes the $E$-state, red denotes the $I$-state, and green denotes the $R$-state. (A) displays the theoretical curves of the model, (B) applies the model to a hypernetwork, (C) to a BA scale-free network, and (D) to an NW small-world network.

Figure 6

Impact of different $\theta$ on the quantities of $I$-state and $E$-state. The (A) displays the effect on the $I$-state, while the (B) shows the effect on the $E$-state. The green curve corresponds to a spreading rate of 0.005, the red to 0.03, and the blue to 0.05.

Figure 7

Effects of different $\epsilon$ on the quantities of $I$-state and $R$-state. The (A) shows the effect of recovering rate on the $I$-state, while the (B) details the effect on the $R$-state. The green curve indicates a $\epsilon$ of 0.04, the red a rate of 0.02, and the blue a rate of 0.01.

Figure 8

Impact of varying average numbers of adjacent nodes on the quantities of $I$-state and $R$-state. The (A) details the effects on the $I$-state, while the (B) details the effects on the $R$-state. The green curve denotes $m=3$, $m_1=7$; the red curve denotes $m=2$, $m_1=5$; the blue curve denotes $m=1$, $m_1=3$.

Figure 9

Impact of different ratios of active ($S_a$) to inactive ($S_i$) nodes on the quantities of $I$-state and $R$-state. The (A) details the effect on the $R$-state, while the (B) details the effect on the $I$-state. The green curve indicates a ratio of $S_a:S_i=4:6$, the red a ratio of $S_a:S_i=3:7$, and the blue a ratio of $S_a:S_i=2:8$.

Figure 10

Time-dependent curves of active users in different information dissemination models at a fixed transmission rate. The blue curve in the figure represents the trend in the number of users in the $I$-state in the SIR model, the red curve represents the trends in the number of users in both the $E$-state and $I$-state in the SEIR model, and the green curve represents the trends in the number of users in the $E$-state and $I$-state in the SSEIR model.

Figure 11

Change curves of different states of the SSEIR model under various real networks. (A) shows the validation of the SSEIR model in a scientific collaboration network, while (B) depicts the validation in a Twitter social network. The figures use green, red, and blue curves to represent the change curves of the $R$-state, $I$-state, and $E$-state, respectively.