Design of facilitated dissociation enables control over cytokine signaling duration

Abstract

Protein design has focused primarily on the design of ground states, ensuring they are sufficiently low energy to be highly populated¹. Designing the kinetics and dynamics of a system requires, in addition, the design of excited states that are traversed in transitions from one low-lying state to another^2,3. This is a challenging task as such states must be sufficiently strained to be poorly populated, but not so strained that they are not populated at all, and because protein design methods have generally focused on creating near-ideal structures^4-7. Here we describe a general approach for designing systems which use an induced-fit power stroke⁸ to generate a structurally frustrated⁹ and strained excited state, allosterically driving protein complex dissociation. X-ray crystallography, double electron-electron resonance spectroscopy, and kinetic binding measurements demonstrate that incorporating excited states enables design of effector-induced increases in dissociation rates as high as 6000-fold. We highlight the power of this approach by designing cytokine mimics which can be dissociated within seconds from their receptors.

Extended Data Fig. 1:. Structural characterization of AS5 and structural frustration of AS1 state BA_X.

a, Crystal structure of AS5 alone (gray) overlaid with the design model of AS5 in state X (blue). Inset shows a detailed view of side chains in the partially-open effector-binding cleft. b, Cocrystal structure of AS5 and peptide effector (gray) overlaid with the design model of the AS5-effector complex in state Y (AS5 in blue, effector in orange). Inset shows the same view of the side chains in the effector-binding cleft as in (a). c, Design model of AS1 in state X (blue) aligned to the partner (pink), showing a minor clash. d, Three cocrystal structures of AS1 (with intact cleft) and partner with methylated lysines (gray) overlaid with the AF2 model of the partner-AS1 complex in state X (AS1 in blue, partner in pink), showing fluctuation in the partner binding conformation.

Extended Data Fig. 2:. DEER characterization of AS1 and AS114.

a, Raw DEER traces (black), foreground fits (colors), and background fits (gray) for AS1 and AS114 with all combinations of partner and effector. Experiments on complexes included the partner, effector, or both in excess over the host at concentrations higher than required to fully form the complex (Fig. S9), and spin labels were placed far from the partner and effector binding sites. Thus, changes in the DEER distance distributions with different combinations of partner and effector should only reflect changes in host conformation. b, Distance distributions from experiment (colors with shaded 95% confidence intervals) and simulated from the structural state represented by the cartoons (black). For AS1, the simulated and experimental distance distributions agree well, further validating that each state adopts its designed conformation. For AS114, the simulations consistently overestimate the experimental distribution by ~5 Å, but the shift in the distance distributions with the effector compared to those without validates the designed conformational change. c, Experimental distance distributions of all states, colored corresponding to (b) and with shaded 95% confidence intervals. For both AS1 and AS114, the ternary complex distribution (green) aligns with the host-effector complex distribution (orange) and not with the host alone (blue) or partner-host complex (pink) distributions, confirming that the ternary complex is primarily in state Y.

Extended Data Fig. 3:. MD characterization of the AS1 ternary complex.

a, Lower Cα RMSD of the MD trajectories from the crystal structure (gray) than from the aligned clashing design models of partner and host-effector complex (black), showing that the MD simulations strain away from the clashing state in a manner similar to the crystal structure. b, Cα RMSD of the switch (blue) and partner (pink) from their position in the crystal structure when the entire structures are aligned. Compared to trajectories 1 and 2, trajectory 3 shows reduced partner deformation and increased switch deformation, showing that these trajectories differ in where they localize strain to resolve the clash. c, Per-residue Cα RMSF of the host (blue), partner (pink), and effector (orange) in the ternary complex computed from each trajectory. The clashing region of the partner (highlighted in gray) shows significant flexibility, according with this region being disordered in the crystal structure. d, Comparison of MD simulations to experimental data. (Left) Crystal conformation of the ternary complex (gray) aligned to representative conformations from each MD trajectory (red, yellow, and light blue). DEER spin label positions are shown in green. In the crystal structure, the clashing region on the partner is disordered. In the MD simulations, though flexible, this region remains mostly ordered, causing additional deformation compared to the crystal structure. Illustrating the differences in strain localization among trajectories shown in panel (b), in the first two trajectories (red and yellow), the switch conformation aligns with the crystal structure and the partner deforms more; in the third trajectory (light blue), the partner conformation aligns with the crystal structure and the switch deforms instead. (Right) experimentally measured DEER distance distribution of the ternary complex (green with shaded 95% confidence interval) and distance distributions simulated from the crystal structure (gray line) or MD trajectories (dashed lines, colors correspond to the conformations shown at left). The distance distribution simulated from the crystal structure aligns with the left peak in the experimental distance distribution, whereas the distance distributions simulated from the MD trajectories span the experimental distance distribution, suggesting that these trajectories more fully sample the space of ternary complex dynamics.

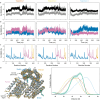
Extended Data Fig. 4:. Modeling strain energy in the ternary complex.

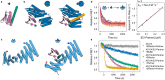
a, Differences in ternary complex geometry for a fast AS1 variant (AS117, left) and a slower variant which yet deforms more in the ternary complex (AS114, right). Design models of host-effector complex in state Y (blue and orange) aligned to the partner (pink) showing the allosteric clash, and (gray) AF2 predictions of the ternary complex aligned to the switch showing how the clash resolves through global strain. To model the strain energy from these structures using Hooke’s law, we measured the global deformation by the angle ($\theta -{\theta }_0$) the partner pivots around some axis (the “pivot axis”) to move from its clashing position to its AF2-predicted strained position. The binder helix in the interface with the partner tends to be positioned near the centerpoint of the deformation (the point around which the centroid of the partner pivots), and the structure of this helix is the same for all variants, so we used the axis of this helix (the “helix axis”) to approximate the orientation of the deforming secondary structure elements. For each variant shown, the left view places the pivot of the partner within the plane of the page (so the pivot axis is normal to the page), and the right view places the helix axis and the pivot axis both within the plane of the page. In the left view, lines are drawn from the pivot axis through the centroids of the clashing and strained partners; the angle between these lines is the angle of global deformation ($\theta -{\theta }_0$). The right view shows the angle between the helix axis and the pivot axis ($\phi$); this is large for the fast variant and small for the slow but highly deforming variant. b, Lack of correlation between predicted magnitude of deformation and the experimental strain energy of the ternary complex for a set of host designs (AS1, AS2, AS5, AS7, and the AS1 variants, plotted as circles colored by their experimental strain energy except for AS101, AS115, AS119, and AS120 which were left out of the analysis in (c) and (d) and are colored gray—34 designs in total). The strain energy can be estimated from the observed accelerated off-rate as follows. $$\text{Experimental}\Delta \Delta G_{\text{ABC}}=RT\text{ln}\frac{K_{\mathrm{D},\text{B:AC}}}{K_{\mathrm{D},\text{B:A},\text{unstrained}}}=RT\text{ln}\frac{k_{\text{off},\text{B:AC}}{k}_{\text{on},\text{B:A},\text{unstrained}}}{k_{\text{off},\text{B:A},\text{unstrained}}{k}_{\text{on},\text{B:AC}}}$$ Making the approximation that $k_{\text{on},\text{B:AC}}=k_{\text{on},\text{B:A},\text{unstrained}}$ and does not vary with $\Delta \Delta G_{\text{ABC}}$ (Fig. S2) simplifies this expression. $$\text{Experimental}\Delta \Delta G_{\text{ABC}}=RT\text{ln}\frac{k_{\text{off},\text{B:AC}}}{k_{\text{off},\text{B:A},\text{unstrained}}}$$ The accelerated off-rate $k_{\text{off},\text{B:AC}}$ is assumed to be the maximum off-rate observed in the facilitated dissociation experiments (Fig. S10). Since the main partner-binder interface does not change across variants, the off-rate of the unstrained interface $k_{\text{off},\text{B:A},\text{unstrained}}$ should be a constant, $k_{\text{base}}$, with one exception: in some variants, the switch fusion may form additional stabilizing interactions with the partner, reducing the base off-rate $k_{\text{off},\text{B:A}}$ (also measured in the facilitated dissociation experiments). These interactions can likely still form in the strained ternary complex to reduce the accelerated off-rate $k_{\text{off},\text{B:AC}}$ by the same factor. Thus, the smaller of $k_{\text{base}}$ and $k_{\text{off},\text{B:A}}$ is used for $k_{\text{off},\text{B:A},\text{unstrained}}$. For $k_{\text{base}}$, a value of 2e–4 s⁻¹ was used because it gave the best correlation between predicted and experimental $\Delta \Delta G_{\text{ABC}}$ described in panel (d). Notably, this value is quite close to the partner off-rate from the unhindered binder fusion LHD101B4, 9e–5 s⁻¹ (Fig. S7). (c) Linear correlation between the “spring constant” $k$ (which relates the experimental strain energy to the magnitude of the predicted deformation) and the perpendicularity of this deformation to the secondary structure elements in the complex for this set of host designs (circles colored as in (b)). A linear regression on the colored points is plotted as a black line. The perpendicularity is computed as the sine of the angle between the pivot axis and the helix axis, and the spring constant is computed using Hooke’s Law as follows. $$\text{Spring Constant}k=\frac{\Delta \Delta G_{\text{ABC}}}{{\left(\theta -{\theta }_0\right)}^2}$$ This relationship suggests that deforming in a stiff direction (against rather than around helices) deforms the partner interface in a more destabilizing direction or better localizes strain to the partner interface instead of distributing the strain throughout the entire protein. d, Agreement between the experimental strain energy and the strain energy estimated entirely from the predicted structure of the strained ternary complex using Hooke’s Law for this set of host designs (circles colored as in (b)). A linear regression on the colored points is plotted as a black line. The spring constant was assumed to depend linearly on the deformation perpendicularity to the secondary structure elements, and the parameters of this correlation (m and b) were varied to fit the following expression to the experimental strain energies. $$\text{Predicted}\Delta \Delta G_{\text{ABC}}=(m\sin (\phi )+b){\left(\theta -{\theta }_0\right)}^2$$ Sources of Error in this Analysis First, in this simple energetic model of facilitated dissociation described here and in Fig. S2, when the effector binds, the energy of the partner dissociation transition state will decrease by the binding energy of the effector. When the effector and partner are uncoupled, the energy of the ternary complex intermediate will decrease by the same amount so the activation barrier for partner dissociation will not change. When strain between the partner and effector is incorporated into the ternary intermediate, its energy will decrease less upon effector binding, reducing the activation barrier for partner dissociation. This simple energetic model thus assumes that the activation barrier for partner dissociation is directly related to the global energy of the ternary complex. In reality, acceleration of partner dissociation will arise from local deformation at the partner interface. Thus, put differently, the simple energetic model assumes that the global deformation is smoothly distributed across the entire protein. This assumption allows us to directly relate the global deformation predicted by AF2 to the local deformation at the partner interface measured by the accelerated partner off-rate. In reality, the deformation is likely not smoothly distributed, and this may at least partially explain the imperfect correlation between the predicted and experimental strain energy of the ternary complex. This is exemplified by how the partner dissociates more slowly from the AS1 ternary complex with the peptide effector than with the 3hb effector (Fig. 2e,f). Despite forming the same interactions and causing the same conformational change as the 3hb, the more deformable peptide appears to less effectively localize strain to the partner once in the ternary complex. Uneven distribution of strain in the ternary complex is also one possible mechanism underlying unidirectional competition in facilitated dissociation systems. Second, our model estimating the protein stiffness anisotropy using the orientation of the secondary structure elements is likely oversimplified. Proteins have finer levels of structure than the orientation of their secondary structure elements. Much like a normal mode analysis, a more sophisticated model could estimate local spring constants for smaller regions of the protein, then compute a strain energy for each region from its predicted deformation. Third, inaccuracies in the AF2 predictions of the strained ternary complex could cause much of the variation between the experimental and predicted strain energies. Clear cases of this, variants AS101, AS115, AS119, and AS120 (gray) which do not follow this correlation were left out of this analysis. We hypothesize that these variants can adopt an alternate, less-strained ternary complex conformation than the high-energy conformation predicted by AF2.

Extended Data Fig. 5:. Construction and characterization of the chain reaction.

a, Design model of E2-partner, comprising the partner LHD101A (with mutations R43V and V69Q) fused to the effector peptide “E2” (cs201B) for hinge cs201. E2 is colored green and LHD101A is colored pink. b, Design models of E2-partner (green/pink) bound to AS114 (blue) in state X showing no clash (left) and in state Y with the effector peptide (orange) showing a strong clash (right). c, Design models of the reporter hinge “H2” (cs201F with mutation E249L (sticks) which increases E2 on-rate and labeled with Alexa Fluors 555 and 647 at positions indicated by stars) in state X (left) and in state Y with E2-partner (right). AS114 and H2 would massively overlap if simultaneously bound to E2-partner, so their binding should be mutually exclusive: AS114 should cage E2 until its release by the effector. d, E2-partner and H2 association rate, measured by a change in FRET efficiency due to the conformational change in H2 upon binding. (Left) FRET time courses (normalized to the initial signal) with varying concentrations of E2-partner and 5 nM H2; data (circles) fit with single exponentials (lines). (Right) apparent on-rates plotted against E2-partner concentration (circles) and a linear fit. The value of the association rate constant (5e+4 M⁻¹s⁻¹) is higher than the reported value (4.5e+3 M⁻¹s⁻¹) for the original hinge cs201F with effector cs201B, suggesting that mutation E249L on H2 biases its conformational pre-equilibrium toward state Y to increase the apparent association rate. e, Additional data for the kinetically governed chain reaction shown in Fig. 4b. In the gray control time course, 500 nM AS114 was added to 20 nM H2, then 1 μM effector and 6 μM partner was added at time 0, showing that none of these components bind to H2 to cause a change in FRET signal. In the other time courses, preincubated 500 nM AS114 and 250 nM E2-partner was added to 20 nM H2, then buffer (blue), 1 μM effector (green), 6 μM partner (pink), or both (orange) were added at time 0. A baseline drift (obtained from 500 nM AS114 after adding 20 nM H2 then at time 0 adding buffer) was subtracted from each time course, and time courses were normalized to the initial signal. The chain reaction proceeds faster when just excess partner is added, likely due to blocking rebinding of E2-partner to AS114 after transient dissociation, but this effect is insufficient to achieve full acceleration. The chain reaction also proceeds faster when just effector is added, but likely due to transient rebinding of E2-partner to re-form the strained ternary complex, this also does not achieve full acceleration. Adding both effector (to accelerate E2-partner dissociation from AS114) and excess partner (to prevent E2-partner rebinding to AS114) is required to fully accelerate the chain reaction. Note that if a single-chain effector is desired to fully accelerate the chain reaction, the effector and partner could be flexibly fused into a single construct. Such a multivalent effector would be reminiscent of CITED2, whose multivalency enables rapid and unidirectional competition against HIF-1α.

Extended Data Fig. 6:. Construction and characterization of rapid sensors.

a, Structural model of the best SARS-CoV-2 sensor construct, comprising AScov (blue), the SmBiTgraft peptide with the effector (orange) and grafted SmBiT (green), LgBiT (gray or cyan), and flexible linkers (black). b, SPR data showing sfGFP-SmBiTgraft binding to AS0 (blue and orange, association phase), slow subsequent dissociation in the absence of partner (blue), and rapid subsequent dissociation upon addition of 10 μM partner (orange) caused by rapid partner binding to form a transient ternary complex, causing the spike at the beginning of the dissociation phase. c–f, Rapidly sensing the partner through a facilitated dissociation mechanism (top), slowly sensing the effector limited by the slow base exchange rate of SmBiTgraft between binding AS0 and LgBiT (middle), and rapidly sensing the SARS-CoV-2 RBD with facilitated dissociation (bottom). c, Schematics showing the mechanism of sensing. d, Luminescence time courses (normalized to the initial signal) of 10 pM sensor construct then at time 0 adding varying concentrations of analyte; data (colors) fit (black) with single exponentials up to the maximum signal for time courses which showed appreciable signal increase. In some time courses, signal slowly decreases due to depletion of luciferase substrate. e, Luminescence signal fold change plotted against analyte concentration. f, Sensor response rate plotted against analyte concentration for time courses which showed appreciable signal increase.

Extended Data Fig. 7:. Detailed functional characterization of ASNeo2.

a, Schematic depiction of labeling strategy for single molecule tracking experiments b, Single molecule trajectories of IL-2Rβ (red), γ_c (blue) and ASNeo2-induced heterodimers (magenta). c, Data from Fig. 5e as boxplots to display datapoint variation including Neo2 (+/− effector) (green and orange, left side) and single molecule tracking experiments with labeled ASNeo2 and γ_c (right side). Sample sizes and independent repeats are: unstimulated: 37 and 3; ASneo2: 32 and 3; ASneo2 + Effector: 33 and 3; neo2: 44 and 4; neo2 + Effector: 37 and 3; labeled ASneo2: 21 and 2; labeled ASneo2 + Effector: 18 and 2. d, Relative dimerization in relation to receptor cell surface density ratio indicates that high dimerization data variance is caused by differing IL-2Rβ to γ_c ratios at the plasma membrane. Even at high γ_c excess, effector-bound ASNeo2 shows no residual affinity for γ_c. e, Diffusion properties of IL-2Rβ and γ_c are reverted to the ground state after addition of effector. f, Immobile particles are increased upon stimulation, but not decreased after effector addition, potentially indicating receptors internalizing in membrane proximal endosomes. For e and f, the left box always corresponds to IL-2Rβ and the right one to γ_c. Sample sizes for d–f are as in c. g, Normalized localization density over time confirms minimal single molecule bleaching in long term single molecule tracking experiments. Sample sizes and independent repeats are: without Effector: 5 and 5; with Effector: 3 and 3. h, i, Dissociation of ASNeo2-induced IL-2Rβ/γ_c dimers at the cell surface upon addition of 10 μM effector as detected by time-lapse single-molecule co-tracking (h) with color-coded corresponding co-trajectories (i). j, k, Conformational change of ASNeo2 bound to the cell surface receptor probed by smFRET. j, FRET efficiency histograms for ASNeo2 E4C/K211C labeled with Cy3B and ATTO643 bound to cells expressing IL-2Rβ and γ_c in the absence (blue) and presence (yellow) of 10 μM effector. Sample sizes are: without Effector: 7; with Effector: 5. h, smFRET co-localizations of one individual cell before the effector was added (left) and after it was added (right) color-coded for FRET efficiency, highlighting the observation of individual molecules. Statistics for c, e and f were performed using two-sided two-sample Kolmogorov–Smirnov tests (not significant (NS), * p < 0.05, *** p < 0.001). Boxplots show the distribution of the dataset, highlighting the median, quartiles, and outliers, with whiskers extending to the range limits. Scale bar in b and i: 5 μm.

Extended Data Fig. 8:. Characterization of cyclic permutations of ASNeo2.

a, Design models of ASNeo2 and selected cyclic permutations in state X, rainbow-colored from N-terminus (blue) to C-terminus (red) to illustrate the protein topology. In ASNeo2, the switch is at the N-terminus and Neo2 is at the C-terminus. In the cyclic permutations, though the relative positions of the switch and Neo2 changes minimally, the switch is in the middle of the protein, part of Neo2 is at the N-terminus, and the other part is at the C-terminus. This way, the regulatory switch cannot degrade without also breaking Neo2. b, SEC purifications performed on a Superdex 200 Increase 10/300 GL column. The cyclic permutations are prone to aggregation during expression, but distinct monomer peaks can be picked out. c, Fast effector concentration–dependent dissociation of γ_c from the ASNeo2-IL-2Rβγ_c complex upon addition of peptide effector. Data (gray) fit (colors) as described in methods (neglecting the accumulation modeling because accumulation on the SPR surface was negligible with these proteins). d, Effective partner off-rates computed from the model fit by ln(2)÷{half-time of γ_c-host interaction} plotted against effector concentration (circles) and fit with hyperbolic equations (black lines).

Fig. 1 ∣. Strategy for designing proteins which reconfigure through facilitated dissociation.

a, b, c, A high affinity interaction can rapidly exchange through facilitated dissociation (lower pathways), but not through mutually exclusive competition (upper pathways). a, Reaction diagram. b, Energy diagram. c, Schematic of induced-fit facilitated dissociation (bottom) compared to slow mutually exclusive competition (top). The host protein (A, subscripted by conformational state X or Y) is shown in blue, the partner (B) in pink, and the effector (C) in orange. d, Schematic of structural frustration resolved through strain in a facilitated dissociation pathway. Hooke’s law can relate the energy of the ternary intermediate to mechanical properties of the protein. e, Examples of design models of proteins designed to undergo a facilitated dissociation process starting from a tightly interacting state X (left) through a structurally frustrated ternary intermediate in state Y (right, solid) aligned to state X (transparent) to show the conformational change.

Fig. 2 ∣. Kinetic characterization of facilitated dissociation in AS1.

a, Slow dissociation of the partner from the host in the absence of effector (solid) and fast dissociation in the presence of effector (dashed) as assessed by SPR. Slow dissociation data (solid gray) fit with a double exponential (pink). b, Kinetic model describing pathways of competition: (top) mutually exclusive competition, (middle) facilitated dissociation with effector binding rate-limited by conformational selection, (bottom) facilitated dissociation with induced-fit effector binding. ${\mathrm{k}}_{\text{off},\text{B:A}}$, ${\mathrm{k}}_{\text{on},\text{BA:C}}$, ${\mathrm{k}}_{\text{switch}}$, and ${\mathrm{k}}_{\text{off},\text{BA:C}}$ are rate constants. c, Cartoon representations of the peptide (left) and 3hb (right) effectors; interface residues shown in gray. d, Circular dichroism (CD) spectra of the peptide and 3hb effectors. e and f, Kinetic characterization of the formation and breakage of the ternary complex intermediate with the peptide (e) and 3hb (f) effectors. (Top left) fast dissociation of the partner from the ternary complex, data (gray) fit with double exponentials (orange/green); (bottom left) effector association to form the ternary complex and extremely slow subsequent dissociation, data (gray) fit with single exponentials (colors) in the association phase; (right) apparent effector on-rates plotted against effector concentration (circles) and a linear (e) or hyperbolic (f) fit. g and h, Kinetic characterization of the full facilitated dissociation pathway with the peptide (g) and 3hb (h) effectors. (Left) effector concentration–dependent dissociation of the partner upon addition of effector, data (gray) fit (colors) as described in methods; (right) effective partner off-rates plotted against effector concentration (circles) and fit with a hyperbolic equation (black line). There is a discrepancy in the EC₅₀ between this partner dissociation experiment and the 3hb association experiment; this could result from the fusion tag used to affix AS1 to the surface competing with the 3hb for binding the cleft, reducing the apparent 3hb on-rate. In a and the left plots of e–h, cartoons show the arrangement of proteins relative to the SPR chip (gray). In the right plots of e–h, cartoons show the mechanism that can be inferred from the data.

Fig. 3 ∣. Structural characterization of AS1.

a, Crystal structure of AS1 alone (gray) overlaid with the design model of AS1 in state X (blue). Inset shows a detailed view of side chains in the partially-open effector-binding cleft. b, Cocrystal structure of AS1 and peptide effector (gray) overlaid with the design model of the AS1-effector complex in state Y (AS1 in blue, effector in orange). Inset shows the same view of the side chains in the effector-binding cleft as in (a). c, (Top) cocrystal structure of AS1 (with intact cleft) and partner with methylated lysines (gray) overlaid with the design model of the partner-AS1 complex in state X (AS1 in blue, partner in pink). (Bottom) cocrystal structure of AS1 (with collapsed cleft) and partner with methylated lysines (gray) overlaid with the design model of the partner-AS0 complex which adopts a state resembling state X* (AS0 in blue, partner in pink). d, Cocrystal structure of the AS1, partner, and peptide effector with methylated lysines (gray) overlaid at the switch region with the design model of the AS1-effector complex in state Y (AS1 in blue, effector in orange) and design model of the partner (pink) aligned to its binding site on the AS1 design model to show the clash. e, (Top) detailed view of the partner interface side chains in the ternary complex (gray) and the partner-AS1 complex (pink) interacting with AS1 (blue). (Bottom) detailed view of the backbone hydrogen bonding in the interfacial strand pairing. The partner-AS1 complex (pink and blue) contains unstrained hydrogen bonds (green); the ternary complex (gray) contains strained hydrogen bonds (red).

Fig. 4 ∣. Modulation and applications of facilitated dissociation.

a, Comparison of three representative designs with different facilitated dissociation behavior. (For each design) (top left) design model of host in state X (blue) aligned to the partner (pink) to show any clash influencing the partner off-rate in the absence of effector; (top right) design model of host-effector complex in state Y (blue and orange) aligned to the partner (pink) to show the designed allosteric clash, and (gray) AF2 prediction of the partner position relative to the switch in the ternary complex to show how the clash resolves through global strain; (bottom) effective partner off-rates plotted against effector concentration (circles) and fit with hyperbolic equations (black lines). b, Slow release of a kinetically trapped effector (upper schematic) and accelerated release through facilitated dissociation (lower schematic) with FRET time courses (normalized to the initial signal) of preincubated 500 nM AS114 and 250 nM E2-partner after adding 20 nM H2 then at time 0 adding 1 μM effector and excess partner (orange) or buffer (blue). A baseline drift (obtained from 500 nM AS114 after adding 20 nM H2 then at time 0 adding buffer) was subtracted from each time course. c, Breakage of a reversible split luciferase through slow direct competition (upper schematic) and faster facilitated dissociation (lower schematic) with luminescence time courses (normalized to the initial signal) of preincubated 100 pM AS1-LgBiT and 20 nM partner-SmBiT after adding 1 μM effector and 20 μM partner (orange) or just 20 μM partner (blue). d, Rapidly sensing SARS-CoV-2 through facilitated dissociation (schematic) with a luminescence time course (normalized to the initial signal) of 10 pM LgBiT-SmBiTgraft-AScov then at time 0 adding 800 nM SARS-CoV-2 RBD (orange).

Fig. 5 ∣. Design and characterization of a rapidly switchable IL-2 mimic.

a, Natural pathways for switching off IL-2 signaling are slow. b, Design concept: through an induced-fit facilitated dissociation pathway, IL-2 signaling could be switched off rapidly. c, Design models of ASNeo2 in state X complexed with IL-2Rβγ_c, the active signaling state (left), which can be quickly switched off by facilitated dissociation through a strained intermediate complex in state Y (right). d, (Left) fast effector concentration–dependent dissociation of γ_c upon addition of effector, data (gray) fit (colors) as described in methods. (Right) effective γ_c off-rates plotted against effector concentration (circles) and fit with a hyperbolic equation (black line). e, Median relative dimerization of IL-2Rβ and γ_c on the cell surface before adding ASNeo2 (gray), after adding 100 nM ASNeo2 (blue), and after later adding 10 μM effector (orange). Data combined from three independent experiments. Error bars represent 95% confidence intervals. Sample sizes are given in Extended Data Fig. 7. f, Time courses of dimerization of IL-2Rβ and γ_c after pre-stimulation with 100 nM ASNeo2 then adding nothing (blue) or 10 μM effector (orange) at room temperature. Each contains three independent time courses each normalized to its average initial relative dimerization. Data fit with a single exponential (black) yielding the rate constant $k_{\text{app}}$. g, Dose-response of STAT5 phosphorylation relative to baseline upon stimulation with ASNeo2 (blue) or ASNeo2 precomplexed with 100x effector (orange) (one biological replicate). h, Time courses of STAT5 phosphorylation relative to baseline after stimulation with 1 nM ASNeo2 for 5 minutes then adding nothing (blue), 10 μM effector (orange), or 40 μM ruxolitinib (green) at 37°C. Three independent time courses were normalized to the signal at time 0, averaged, and renormalized to the average baseline signal. Shaded areas represent 95% confidence intervals. Some batches of cells were unresponsive to stimulation; data from these batches were excluded from analysis.