A multiobjective evolutionary algorithm for optimizing the small-world property
- PMID: 39625908
- PMCID: PMC11614276
- DOI: 10.1371/journal.pone.0313757
A multiobjective evolutionary algorithm for optimizing the small-world property
Abstract
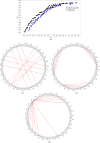
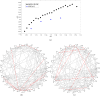
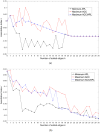
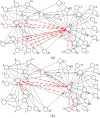
Small-world effect plays an important role in the field of network science, and optimizing the small-world property has been a focus, which has many applications in computational social science. In the present study, we model the problem of optimizing small-world property as a multiobjective optimization, where the average clustering coefficient and average path length are optimized separately and simultaneously. A novel method for optimizing small-world property is then proposed based on the multiobjective evolutionary algorithm with decomposition. Experimental results have proved that the presented method is capable of solving this problem efficiently, where a uniform distribution of solutions on the Pareto-optional front can be generated. The optimization results are further discussed to find specific paths for optimizing different objective functions. In general, adding edges within the same community is helpful for promoting ACC, while adding edges between different communities is beneficial for reducing APL. The optimization on networks with the feature of community structure is more remarkable, but community structure has less impact on the optimization when the internal community is triangles-saturated.
Copyright: © 2024 Zhang, Zhu. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
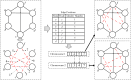

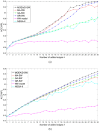
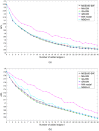
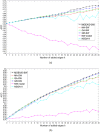
Similar articles
-
Decomposition-based multiobjective evolutionary algorithm for community detection in dynamic social networks.ScientificWorldJournal. 2014 Mar 2;2014:402345. doi: 10.1155/2014/402345. eCollection 2014. ScientificWorldJournal. 2014. PMID: 24723806 Free PMC article.
-
Evolutionary Multiobjective Clustering and Its Applications to Patient Stratification.IEEE Trans Cybern. 2019 May;49(5):1680-1693. doi: 10.1109/TCYB.2018.2817480. Epub 2018 Apr 2. IEEE Trans Cybern. 2019. PMID: 29993679
-
An Opposition-Based Evolutionary Algorithm for Many-Objective Optimization with Adaptive Clustering Mechanism.Comput Intell Neurosci. 2019 May 2;2019:5126239. doi: 10.1155/2019/5126239. eCollection 2019. Comput Intell Neurosci. 2019. PMID: 31191632 Free PMC article.
-
Runtime Analysis of Single- and Multiobjective Evolutionary Algorithms for Chance-Constrained Optimization Problems with Normally Distributed Random Variables.Evol Comput. 2025 Jun 2;33(2):191-214. doi: 10.1162/evco_a_00355. Evol Comput. 2025. PMID: 39101892
-
A Review of Surrogate Assisted Multiobjective Evolutionary Algorithms.Comput Intell Neurosci. 2016;2016:9420460. doi: 10.1155/2016/9420460. Epub 2016 Jun 12. Comput Intell Neurosci. 2016. PMID: 27382366 Free PMC article. Review.
References
-
- Du W., Li G., and He X., “Network structure optimization for social networks by minimizing the average path length,” Computing, vol. 104, no. 6, pp. 1461–1480, 2022.
-
- Du H., Fan J., He X., and Feldman M. W., “A genetic simulated annealing algorithm to optimize the small-world network generating process,” Complexity, vol. 2018, pp. 1–12, 2018.
-
- Milgram S., “The Small World Problem,” Psychol Today, vol. 1, no. 1, pp. 60–67, 1967.
MeSH terms
LinkOut - more resources
Full Text Sources

