From 3D to 2D and back again
- PMID: 39634355
- PMCID: PMC11501230
- DOI: 10.1515/nanoph-2022-0512
From 3D to 2D and back again
Abstract
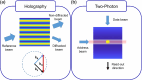
The prospect of massive parallelism of optics enabling fast and low energy cost operations is attracting interest for novel photonic circuits where 3-dimensional (3D) implementations have a high potential for scalability. Since the technology for data input-output channels is 2-dimensional (2D), there is an unavoidable need to take 2D-nD transformations into account. Similarly, the 3D-2D and its reverse transformations are also tackled in a variety of fields such as optical tomography, additive manufacturing, and 3D optical memories. Here, we review how these 3D-2D transformations are tackled using iterative techniques and neural networks. This high-level comparison across different, yet related fields could yield a useful perspective for 3D optical design.
Keywords: 3D optical memory; additive manufacturing; inverse design; optical tomography; photonic circuit design.
© 2022 the author(s), published by De Gruyter, Berlin/Boston.
Figures



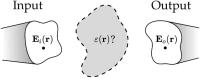


References
-
- Shen Y., Harris N. C., Skirlo S., et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics . 2017;11(7):441–446. doi: 10.1038/nphoton.2017.93. - DOI
-
- Xu X., Ren G., Feleppa T., et al. Self-calibrating programmable photonic integrated circuits. Nat. Photonics . 2022;16(8):595–602. doi: 10.1038/s41566-022-01020-z. - DOI
Publication types
LinkOut - more resources
Full Text Sources
