Nonlocal effects in temporal metamaterials

Abstract

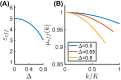
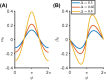
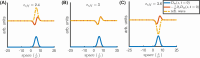
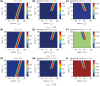
Nonlocality is a fundamental concept in photonics. For instance, nonlocal wave-matter interactions in spatially modulated metamaterials enable novel effects, such as giant electromagnetic chirality, artificial magnetism, and negative refraction. Here, we investigate the effects induced by spatial nonlocality in temporal metamaterials, i.e., media with a dielectric permittivity rapidly modulated in time. Via a rigorous multiscale approach, we introduce a general and compact formalism for the nonlocal effective medium theory of temporally periodic metamaterials. In particular, we study two scenarios: (i) a periodic temporal modulation, and (ii) a temporal boundary where the permittivity is abruptly changed in time and subject to periodic modulation. We show that these configurations can give rise to peculiar nonlocal effects, and we highlight the similarities and differences with respect to the spatial-metamaterial counterparts. Interestingly, by tailoring the effective boundary wave-matter interactions, we also identify an intriguing configuration for which a temporal metamaterial can perform the first-order derivative of an incident wavepacket. Our theoretical results, backed by full-wave numerical simulations, introduce key physical ingredients that may pave the way for novel applications. By fully exploiting the time-reversal symmetry breaking, nonlocal temporal metamaterials promise a great potential for efficient, tunable optical computing devices.

Keywords: analog computing; effective medium; metamaterials; nonlocality; optical magnetism; time-reversal symmetry.

Figure 1:

Comparison between the predictions from the full-wave theory and both local an nonlocal EMT models for a temporal metamaterial with relative permittivity as in Eq. (10), with $\overline{\epsilon }=5$ . (A)–(C) Normalized angular frequency ω/Ω as function of the normalized wavenumber k/K, for Δ = 0.5, 0.65, and 0.8, respectively.The light-blue shaded area indicates the region where the nonlocal EMT works well (≲10% error with respect to full-wave theory).

Figure 2:

Effective parameters for the temporal metamaterial considered in Figure 1. (A) Effective relative permittivity ϵ _eff as a function of Δ; (B) effective relative permeability μ _eff(k) as a function of k/K, for different values of the modulation depth Δ. Note that μ _eff(k) is only shown within the region where the nonlocal EMT holds (≲10% error with respect to full-wave theory).

Figure 3:

Nonlocal temporal boundary. (A) and (B) Nonlocal effective boundary parameters α ₀ and β ₀, respectively, as a function of the modulation phase ϕ. Here, t ₀ = 0, and a metamaterial with the permittivity profile in Eq. (10) is considered with $\overline{\epsilon }=5$ .

Figure 4:

Nonlocal contributions in Eq. (14) as a function of k/K and ϕ, for Δ = 0.5 ((A) and (B)), Δ = 0.65 ((C) and (D)), and Δ = 0.8 ((E) and (F)). Here, t ₀ = 0 and a temporal metamaterial with the permittivity profile in Eq. (10) is considered, with $\overline{\epsilon }=5$ . The parameters are only shown within the region where the nonlocal EMT holds (≲10% error with respect to full-wave theory).

Figure 5:

Spatial profiles of reflected (backward) pulses D _r (z, t ₁) (t ₁ ≃ 20τ) in the configuration described by Eqs. (11) and (10), with ɛ ₁ = 3, t ₀ = 10τ, ϕ = 3π/2, Δ = 0.8, and $\overline{\epsilon }=\mathrm{4,5,6}$ shown in panels (A)–(C), respectively. The blue curve represents the incident pulse profile D _in(z, t = 0), and the backward pulse D _r (z, t ₁) (orange-dashed) is superposed to the first spatial derivative of D _in(z, t = 0) (red).

Figure 6:

As in Figure 5, but space-time maps of the electric induction D and the corresponding forward (D _t ) and backward (D _r ) components for ɛ _eff = 2.4 ((A)–(C)), ɛ _eff = 3 ((D)–(F)), and ɛ _eff = 3.6 ((G)–(I)).

Figure 7:

Comparison between the backward wavepacket profiles predicted by full-wave simulations, local and non-local EMTs. The considered temporal dielectric profiles ensuring the impedance-matching conditions [i.e., the configuration described by Eqs. (11) and (10), with ɛ ₁ = 3, t ₀ = 10τ, Δ = 0.8, and $\overline{\epsilon }=5$ ] is plotted with ϕ = 3π/2 (panel (A)), ϕ = 0.67π (panel (D)), and ϕ = π (panel (G)). Panels (B), (E), and (H) show the corresponding normalized electric inductions D _r/D ₀ for the backward pulses. Panels (C), (F), and (I) show the corresponding normalized electric fields ɛ ₀ E _r/D ₀. All temporal profiles are evaluated at z = −30cτ.