Deep learning for optical tweezers

Abstract

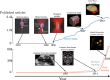
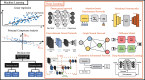
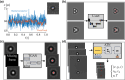
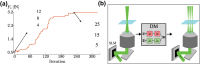
Optical tweezers exploit light-matter interactions to trap particles ranging from single atoms to micrometer-sized eukaryotic cells. For this reason, optical tweezers are a ubiquitous tool in physics, biology, and nanotechnology. Recently, the use of deep learning has started to enhance optical tweezers by improving their design, calibration, and real-time control as well as the tracking and analysis of the trapped objects, often outperforming classical methods thanks to the higher computational speed and versatility of deep learning. In this perspective, we show how cutting-edge deep learning approaches can remarkably improve optical tweezers, and explore the exciting, new future possibilities enabled by this dynamic synergy. Furthermore, we offer guidelines on integrating deep learning with optical trapping and optical manipulation in a reliable and trustworthy way.

Keywords: deep learning; optical manipulation; optical tweezers.

Figure 1:

The rise of optical trapping and deep learning in scientific publications. Number of articles published per year that use “optical trapping” (blue line), “machine learning” (gray line), or “deep learning” (orange line) in their title, abstract, or keywords. Milestones in the development of these fields are highlighted with illustrations. Data obtained from Web of Science^TM on November 2023.

Figure 2:

Machine learning and deep learning. Deep learning (orange rectangle) is a subset of machine learning (black rectangle). Machine learning approaches include linear regression, principal component analysis, and decision trees. Deep learning approaches include dense neural networks, convolutional neural networks, U-nets, attention-based transformer networks, graph neural networks, generative adversarial networks, variational autoencoders, diffusion model, and deep reinforcement learning.

Figure 3:

Deep learning for particle tracking. (a) Trajectory of an optically trapped particle obtained from a noisy video by DeepTrack (orange) compared to that obtained with the classical radial symmetry algorithm (blue line). Reproduced from Ref. [41]. (b) As potential application, a U-net can be used to track trapped particles that approach one to the other also when one particle overlaps with the other (defocused particle in the bottom picture on the left). (c) As potential application, a TGAN can fill missing frames in a video file (e.g., due to uneven sampling rate) and track the particles allowing the applications of calibration methods that require a constant sampling rate (e.g., those based on power spectral density, autocorrelation functions, and mean squared displacement). (d) As potential application, an ATN can find the trajectory of optically trapped particles in a video file and use it to determine the physical properties of the particles, such as their refractive index n _p and radius r, as well as information about the immersion media, such as its viscosity η and its temperature T.

Figure 4:

Deep learning for trajectory analysis and calibration. (a) A convolutional neural network is trained on simulated data in order to extrapolate from the particle trajectory the medium viscosity η. Reproduced from Ref. [113]. (b) As potential application, a diffusion model can be used to extract information about the diffusion processes of a trapped particle when there are missing points in the trajectory. (c) The DeepCalib method used a recurrent neural network trained on simulated data to extract the trap stiffness for a microparticle held in a harmonic potential. Reproduced from Ref. [40]. (d) As potential application, an attention-based transformer network can determine whether a trapped particle is in thermal equilibrium or in a non-equilibrium condition.

Figure 5:

Deep learning for optical force calculation. (a) Experimental (black symbols) and neural-network-simulated (orange line) rotation rates ω as a function of the parameter α of the superposition of two Laguerre–Gaussian beams, α LG_0,+5 + (1 − α) LG_0,−5. The error bars represent standard errors. Reproduced from Ref. [38]. (b) A dense neural network calculates the optical forces in the geometrical-optics approximation increasing not only the calculation speed but also the accuracy when compared to the conventional geometrical-optics approach. The neural network (orange line) has been trained with data generated with geometrical optics using 100 rays (purple line) and approximates much better the exact solution (black line). Reproduced from Ref. [39]. (c) As potential application, a GNN could evaluate the force field (red arrows in the right panel) directly from images of the optical field (on the left). (d) As potential application, a CNN could be used to evaluate and optimize the trapping force directly from the 2D design of a near-field optical trap.

Figure 6:

Real-time control of optical tweezers with deep learning. (a) Sketch of a trapped particle moved in real time by a neural network to avoid both physical (defocused particles) and virtual (white hollow circles) obstacles. The red solid line represents the trajectory, the white arrows the direction of the motion, and the green cross the destination point of the particle. Reproduced from Ref. [122]. (b) As potential application, digital twins and VAEs can be used to automatize trapping experiments of only particles with specific properties. (c) As potential application, deep reinforcement learning and Bayesian modeling can be used to automatize the DNA pulling experiment done with two optical traps. (d) As potential application, U-net and Bayesian modeling can improve the process of filling micro-holes in a microfluidic chamber with particles in order to create microstructures.

Figure 7:

Deep learning for designing optical tweezers. (a) The design of a nanoaperture is optimized using simulated annealing. The algorithm iteratively updates the shape to find the best one for optical trapping. Reproduced from Ref. [127]. (b) As potential application, a diffusion model could be used in combination with a spatial light modulator to trap multiple particles and enhance the focusing, and therefore the trapping force.