Gauge-independent emission spectra and quantum correlations in the ultrastrong coupling regime of open system cavity-QED

Abstract

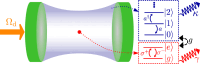
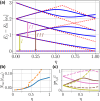
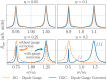
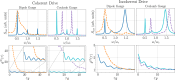
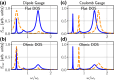
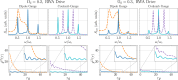
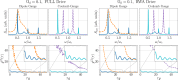
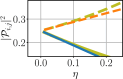
A quantum dipole interacting with an optical cavity is one of the key models in cavity quantum electrodynamics (cavity-QED). To treat this system theoretically, the typical approach is to truncate the dipole to two levels. However, it has been shown that in the ultrastrong-coupling regime, this truncation naively destroys gauge invariance. By truncating in a manner consistent with the gauge principle, we introduce master equations for open systems to compute gauge-invariant emission spectra, photon flux rates, and quantum correlation functions which show significant disagreement with previous results obtained using the standard quantum Rabi model. Explicit examples are shown using both the dipole gauge and the Coulomb gauge.

Keywords: cavity-QED; gauge invariance; master equations; open systems; quantum Rabi model; ultrastrong coupling.

Figure 1:

Schematic of a generic cavity-QED system. The optical cavity mode has quantized energy levels (in blue), with a decay rate κ. The matter system is a truncated TLS (in red), with a possible spontaneous emission decay rate γ. The two systems have a coherent coupling strength g. A coherent laser (in orange) drives the system with Rabi frequency Ω_d.

Figure 2:

Example energy eigenvalues, as well as steady state excitation numbers and selected transitions rates (with and without gauge corrections). (a) The energy eigenvalues of the six lowest states of the QRM (blue, solid) and the JC model (red, dotted). Arrows mark transitions of interest, placed at arbitrary locations on the η-axis, (b) steady state excitation number for incoherent driving (cf. Figure 3), and (c) selected transition rates, with colors matching the arrows in (a). On the bottom two panels, solid (dashed) lines are with (without) the gauge correction in the dipole gauge. Note a sudden increase of N _cav near η ≈ 0.4 when states 2 and 3 cross.

Figure 3:

Cavity spectra outside the RWA (QRM) with DG model (orange dashed line), and DGC model (with gauge correction, blue line) for varying η and weak incoherent driving: P _inc = 0.01g. Spectra are normalized to have the same maxima. Other system parameters are κ = 0.25g, and ω _L = ω _c = ω ₀. Note a small change with the DG corrected model even below the USC regime (η = 0.05).

Figure 4:

Direct comparison between master equation results using the dipole and Coulomb gauges at η = 0.5, for both coherent and incoherent excitation, showing the profound effect of the gauge correction and how this manifests in identical spectra (top) and g ⁽²⁾(τ) correlation functions (bottom). Solid and dashed curves are with and without the gauge correction, respectively. For the coherent drive (left), we use Ω_d = 0.1g, and the incoherent pumping (right) is the same as in Figure 3 (P _inc = 0.01g).

Figure 5:

The computed cavity spectra using the dipole gauge (left) and Coulomb gauge (right), with a flat DOS [κ(ω) = κ, panels (a), (c)] and an Ohmic DOS [κ(ω) = κω/ω _c , panels (b), (d)] using the generalized master equation [see Eqs. (A9) and (A10) in Appendix A]. In both cases, the effect of the gauge correction (solid lines versus dashed lines) is dramatic. We use the same parameters as in Figure 2 of the main text, with incoherent driving, and parameters η = 0.5 and κ = 0.25g. Notably, in all cases, regardless of the spectral function, the corrected dipole gauge and corrected Coulomb gauge results are identical.

Figure 6:

Left four panels show cavity spectra and g ⁽²⁾(τ) for Ω_d = 0.2g, and the right four panels are for Ω_d = 0.3g (cf. Figure 4 of the main text and also below). Solid lines show the gauge corrected master equation results.

Figure 7:

Cavity spectra and g ⁽²⁾ with Ω_d = 0.1g coherent pumping, using a full cosine excitation (left), and an RWA for the pumping term (right, as also shown in Figure 4 of the main text). Solid lines show the gauge corrected master equation results.

Figure 8:

Here we show the full numerical calculations as shown in Figure 2(c) of the main text with (olive solid curve) and without gauge corrections (olive dashed dashed). We also show the BS models, up to first order, again with (blue solid curve, 1/4(1 − 5η/2)) and without gauge corrections (orange dashed curve, 1/4(1 + 3η/2)). The general trends at lower η are well represented.

Figure 9:

A zoom in of the full numerical spectra (solid curves), with (blue solid curve) and without (orange solid curve) the gauge correction, compared with the analytical solution in Eq. (E16) (dashed curves), again with (pink dashed curve) and without (brown dashed curve) the gauge correction. Parameters are the same as in the main text, with κ = 0.25g, though we use a slightly smaller driving strength to ensure the WEA remains valid, P _inc = 0.00025g.