Conditional cooperation with longer memory

Abstract

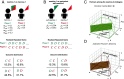
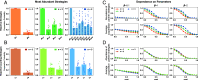
Direct reciprocity is a wide-spread mechanism for the evolution of cooperation. In repeated interactions, players can condition their behavior on previous outcomes. A well-known approach is given by reactive strategies, which respond to the coplayer's previous move. Here, we extend reactive strategies to longer memories. A reactive-n strategy takes into account the sequence of the last n moves of the coplayer. A reactive-n counting strategy responds to how often the coplayer cooperated during the last n rounds. We derive an algorithm to identify the partner strategies within these strategy sets. Partner strategies are those that ensure mutual cooperation without exploitation. We give explicit conditions for all partner strategies among reactive-2, reactive-3 strategies, and reactive-n counting strategies. To further explore the role of memory, we perform evolutionary simulations. We vary several key parameters, such as the cost-to-benefit ratio of cooperation, the error rate, and the strength of selection. Within the strategy sets we consider, we find that longer memory tends to promote cooperation. This positive effect of memory is particularly pronounced when individuals take into account the precise sequence of moves.

Keywords: direct reciprocity; evolution of cooperation; evolutionary game theory; prisoner’s dilemma.

Fig. 1.

The repeated prisoner’s dilemma among players with finite memory. (A) In the repeated prisoner’s dilemma, in each round two players independently decide whether to cooperate (C) or to defect (D). (B) When players adopt memory-1 strategies, their decisions depend on the entire outcome of the previous round. That is, they consider both their own and the coplayer’s previous action. (C) When players adopt a reactive-n strategy, they make their decisions based on the coplayer’s actions during the past n rounds. (D) A self-reactive-n strategy is contingent on the player’s own actions during the past n rounds. (E) To illustrate these concepts, we show a game between a player with a reactive-1 strategy (Top) and an arbitrary player (Bottom). Reactive-1 strategies can be represented as a vector $\mathbf{p}=(p_C,p_D)$. The entry p_C is the probability of cooperating given the coplayer cooperated in the previous round. The entry p_D is the cooperation probability after the coplayer defected. (F) Now, the Top player adopts a self-reactive-1 strategy, $\tilde{\mathbf{p}}=({\tilde{p}}_C,{\tilde{p}}_D)$. Here, the player’s cooperation probability depends on its own previous action.

Fig. 2.

Characterizing partners among the reactive-n strategies. (A and B) To characterize the reactive-n partner strategies, we prove the following result. Suppose the focal player adopts a reactive-n strategy. Then, for any strategy of the opponent (with arbitrary memory), one can find an associated self-reactive-n strategy that yields the same payoffs. Here, we show an example. Player 1 uses a reactive-1 strategy against player 2 with a memory-1 strategy. Our result implies that player 2 can switch to a well-defined self-reactive-1 strategy. This switch leaves the outcome distribution unchanged. In both cases, players are equally likely to experience mutual cooperation, unilateral cooperation, or mutual defection in the long run. (C) Based on this insight, we can explicitly characterize the reactive-2 partner strategies (with $p_{\mathit{CC}}=1$). Here, we represent the corresponding conditions in Eq. 1 for a donation game with $b/c=2$. Among the reactive-2 strategies, the counting strategies correspond to the subset with $p_{\mathit{CD}}=p_{\mathit{DC}}$. Counting strategies only depend on how often the coplayer cooperated in the past, not on the timing of cooperation. (D) Similarly, we can also characterize the reactive-2 partner strategies for the general prisoner’s dilemma. Here, we use the payoff matrix of Axelrod (7).

Fig. 3.

Conditions for partners among reactive-2 and reactive-3 strategies. (A) Pure self-reactive strategies generate simple repetitive sequences of actions that are independent of the coplayer. For example, in the case of n = 2, the pure self-reactive strategy $\tilde{\mathbf{p}}=(0,1)$ generates the indefinitely repeated alternating sequence DC. (B) For a nice reactive strategy p to be a partner, all of these self-reactive strategies need to achieve at most the mutual cooperation payoff against p. This leads to necessary conditions for p to be a partner, which we show here for n = 2, and n = 3. Interestingly, we prove that these necessary conditions are also sufficient, see SI Appendix. (C) To derive the conditions, we consider the average payoff of each repetitive sequence. In the Top panel, we illustrate an example for n = 2. Here, the repetitive sequence DC plays against the reactive strategy $\mathbf{p}=(1,p_{\mathit{CD}},p_{\mathit{DC}},p_{\mathit{DD}})$. In odd rounds, the sequence player receives a benefit b with probability p_DC, without paying any cost. In even rounds, the player receives the benefit b with probability p_CD, while paying a cost c. Over the course of two consecutive rounds, the player thus receives $(p_{\mathit{DC}}+p_{\mathit{CD}})b-c$. This payoff needs to be smaller or equal than what a partner strategy achieves against itself, which is $2(b-c)$. This leads to condition ($\ast$). In the Bottom panel, we illustrate a similar example for n = 3, explaining condition (†).

Fig. 4.

Evolutionary dynamics of reactive-n strategies. To explore the evolutionary dynamics among reactive-n strategies, we run simulations based on the method of Imhof and Nowak (68). This method assumes rare mutations. Every time a mutant strategy appears, it goes extinct or fixes before the arrival of the next mutant strategy. (A and B) We run twenty independent simulations for reactive-n strategies and for reactive-n counting strategies. For each simulation, we record the most abundant strategy (the strategy that resisted most mutants). The respective average cooperation probabilities are in line with the conditions for partner strategies. (C and D) With additional simulations, we explore the average abundance of partner strategies and the population’s average cooperation rate. For a given resident strategy to be classified as a partner by our simulation, it needs to satisfy all inequalities in the respective characterization. In addition, it needs to cooperate after full cooperation with a probability of at least 95%. For all considered parameter values, we only observe high cooperation rates when partner strategies evolve. Simulations are based on a donation game with b = 1, c = 0.5, a selection strength β = 1, and a population size N = 100, unless noted otherwise. For n equal to 1 and 2, simulations are run for ${10}^7$ time steps. For n = 3 we use $2·{10}^7$ time steps.