Functional Mixed Membership Models
- PMID: 39651451
- PMCID: PMC11623444
- DOI: 10.1080/10618600.2024.2304633
Functional Mixed Membership Models
Abstract
Mixed membership models, or partial membership models, are a flexible unsupervised learning method that allows each observation to belong to multiple clusters. In this paper, we propose a Bayesian mixed membership model for functional data. By using the multivariate Karhunen-Loève theorem, we are able to derive a scalable representation of Gaussian processes that maintains data-driven learning of the covariance structure. Within this framework, we establish conditional posterior consistency given a known feature allocation matrix. Compared to previous work on mixed membership models, our proposal allows for increased modeling flexibility, with the benefit of a directly interpretable mean and covariance structure. Our work is motivated by studies in functional brain imaging through electroencephalography (EEG) of children with autism spectrum disorder (ASD). In this context, our work formalizes the clinical notion of "spectrum" in terms of feature membership proportions. Supplementary materials, including proofs, are available online. The R package BayesFMMM is available to fit functional mixed membership models.
Keywords: Bayesian Methods; EEG; Functional Data; Mixed Membership Models; Neuroimaging.
Figures


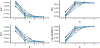
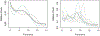

References
-
- Azar Y, Fiat A, Karlin A, McSherry F and Saia J (2001), Spectral analysis of data, in ‘Proceedings of the thirty-third annual ACM symposium on Theory of computing’, pp. 619–626.
-
- Blei D, Ng A and Jordan M (2003), ‘Latent Dirichlet allocation’, JMLR.
-
- Broderick T, Pitman J and Jordan M (2013), ‘Feature allocations, probability functions, and paintboxes’, Bayesian Analysis 8(4), 801–836.
-
- Chen Y, He S, Yang Y and Liang F (2022), ‘Learning topic models: Identifiability and finite-sample analysis’, Journal of the American Statistical Association pp. 1–16. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
