Preserving friendships in school contacts: An algorithm to construct synthetic temporal networks for epidemic modelling
- PMID: 39652593
- PMCID: PMC11676524
- DOI: 10.1371/journal.pcbi.1012661
Preserving friendships in school contacts: An algorithm to construct synthetic temporal networks for epidemic modelling
Abstract
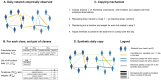
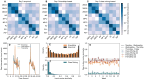
High-resolution temporal data on contacts between hosts provide crucial information on the mixing patterns underlying infectious disease transmission. Publicly available data sets of contact data are however typically recorded over short time windows with respect to the duration of an epidemic. To inform models of disease transmission, data are thus often repeated several times, yielding synthetic data covering long enough timescales. Looping over short term data to approximate contact patterns on longer timescales can lead to unrealistic transmission chains because of the deterministic repetition of all contacts, without any renewal of the contact partners of each individual between successive periods. Real contacts indeed include a combination of regularly repeated contacts (e.g., due to friendship relations) and of more casual ones. In this paper, we propose an algorithm to longitudinally extend contact data recorded in a school setting, taking into account this dual aspect of contacts and in particular the presence of repeated contacts due to friendships. To illustrate the interest of such an algorithm, we then simulate the spread of SARS-CoV-2 on our synthetic contacts using an agent-based model specific to the school setting. We compare the results with simulations performed on synthetic data extended with simpler algorithms to determine the impact of preserving friendships in the data extension method. Notably, the preservation of friendships does not strongly affect transmission routes between classes in the school but leads to different infection pathways between individual students. Our results moreover indicate that gathering contact data during two days in a population is sufficient to generate realistic synthetic contact sequences between individuals in that population on longer timescales. The proposed tool will allow modellers to leverage existing contact data, and contributes to the design of optimal future field data collection.
Copyright: © 2024 Calmon et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



Similar articles
-
An algorithm to build synthetic temporal contact networks based on close-proximity interactions data.PLoS Comput Biol. 2024 Jun 13;20(6):e1012227. doi: 10.1371/journal.pcbi.1012227. eCollection 2024 Jun. PLoS Comput Biol. 2024. PMID: 38870216 Free PMC article.
-
Determining the optimal strategy for reopening schools, the impact of test and trace interventions, and the risk of occurrence of a second COVID-19 epidemic wave in the UK: a modelling study.Lancet Child Adolesc Health. 2020 Nov;4(11):817-827. doi: 10.1016/S2352-4642(20)30250-9. Epub 2020 Aug 3. Lancet Child Adolesc Health. 2020. PMID: 32758453 Free PMC article.
-
Digital contact tracing technologies in epidemics: a rapid review.Cochrane Database Syst Rev. 2020 Aug 18;8(8):CD013699. doi: 10.1002/14651858.CD013699. Cochrane Database Syst Rev. 2020. PMID: 33502000 Free PMC article.
-
Contact Patterns in a High School: A Comparison between Data Collected Using Wearable Sensors, Contact Diaries and Friendship Surveys.PLoS One. 2015 Sep 1;10(9):e0136497. doi: 10.1371/journal.pone.0136497. eCollection 2015. PLoS One. 2015. PMID: 26325289 Free PMC article.
-
A Data-Driven Simulation of the Exposure Notification Cascade for Digital Contact Tracing of SARS-CoV-2 in Zurich, Switzerland.JAMA Netw Open. 2021 Apr 1;4(4):e218184. doi: 10.1001/jamanetworkopen.2021.8184. JAMA Netw Open. 2021. PMID: 33929521 Free PMC article.
Cited by
-
Epidemic Dynamics and Intervention Measures in Campus Settings Based on Multilayer Temporal Networks.Entropy (Basel). 2025 May 21;27(5):543. doi: 10.3390/e27050543. Entropy (Basel). 2025. PMID: 40422497 Free PMC article.
References
-
- World Health Organisation. Global technical consultation report on proposed terminology for pathogens that transmit through the air; 2024. [Cited 2024 October 7]. Available from: https://www.who.int/publications/m/item/global-technical-consultation-re....
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Miscellaneous

