A near-tight lower bound on the density of forward sampling schemes

Abstract

Motivation: Sampling k-mers is a ubiquitous task in sequence analysis algorithms. Sampling schemes such as the often-used random minimizer scheme are particularly appealing as they guarantee at least one k-mer is selected out of every w consecutive k-mers. Sampling fewer k-mers often leads to an increase in efficiency of downstream methods. Thus, developing schemes that have low density, i.e. have a small proportion of sampled k-mers, is an active area of research. After over a decade of consistent efforts in both decreasing the density of practical schemes and increasing the lower bound on the best possible density, there is still a large gap between the two.

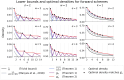
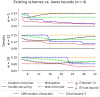
Results: We prove a near-tight lower bound on the density of forward sampling schemes, a class of schemes that generalizes minimizer schemes. For small w and k, we observe that our bound is tight when k≡1(mod w). For large w and k, the bound can be approximated by 1w+k⌈w+kw⌉. Importantly, our lower bound implies that existing schemes are much closer to achieving optimal density than previously known. For example, with the current default minimap2 HiFi settings w = 19 and k = 19, we show that the best known scheme for these parameters, the double decycling-set-based minimizer of Pellow et al. is at most 3% denser than optimal, compared to the previous gap of at most 50%. Furthermore, when k≡1(mod w) and the alphabet size σ goes to ∞, we show that mod-minimizers introduced by Groot Koerkamp and Pibiri achieve optimal density matching our lower bound.

Availability and implementation: Minimizer implementations: github.com/RagnarGrootKoerkamp/minimizers ILP and analysis: github.com/treangenlab/sampling-scheme-analysis.

Figure 1.

(a) A De Bruijn graph B₃ corresponding to a minimum density $(w=2,k=2)$-forward scheme. The underlined characters in each vertex represent the 2-mer that is selected for that window. The solid edges represent the charged contexts and the edge colors represent the pure cycles in B₄ (not in B₃ itself). For characters c_i, each edge $(c_0{c}_1{c}_2,c{\prime }_{0}c{\prime }_{1}c{\prime }_2)$ in B₃ corresponds to the vertex $c_0{c}_1{c}_{2}c{\prime }_2$ in B₄. (b) The corresponding $(w=2,\ell =4)$-UHS in B₄. The vertices are partitioned by color, representing the pure-cycles. The 2-mer(s) selected in each context are underlined. The vertices with a double border represent the charged edges in B₃ in (a) and the corresponding (2, 4)-UHS. Each pure cycle c has at least $\lceil \left|c\right|/w\rceil$ vertices in the UHS.

Figure 2.

Comparison of forward scheme lower bounds and optimal densities for small w, k, and σ. Optimal densities were obtained via the ILP and are plotted as black circles that are solid when the optimal density matches our lower bound, $g{\prime }_{\sigma }$, and hollow otherwise. Each column corresponds to a parameter being fixed to the lowest non-trivial value, i.e., σ = 2 in the first column, w = 2 in the second column, and k = 1 in the third column. Note that the x-axis in the third column corresponds to w, not k.

Figure 3.

Comparison of existing schemes to lower bounds with practical parameters. Densities are calculated by applying each scheme to a random sequence of 10 million characters over an alphabet of size σ = 4 (dotted lines) and are compared with the corresponding proportion of sampled k-mers on the human Y chromosome (Rhie et al. 2023) (soft lines). The mod-minimizer uses parameter r = 4, and miniception uses parameter $\max (4,k-w)$. The window sizes 5 and 19 are the default window sizes for Kraken2 (Wood et al. 2019) and minimap2 (-ax hifi) (Li 2018), respectively. For SSHash, w = 12 was the window size used when indexing the human genome (Pibiri 2022).