Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Mar 21:12:102652.
doi: 10.1016/j.mex.2024.102652. eCollection 2024 Jun.

The performance of mixed truncated spline-local linear nonparametric regression model for longitudinal data

Idhia Sriliana  1   2 , I Nyoman Budiantara  1 , Vita Ratnasari  1
Affiliations

The performance of mixed truncated spline-local linear nonparametric regression model for longitudinal data

Idhia Sriliana et al. MethodsX. .

Abstract

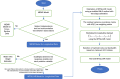
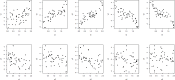
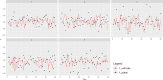
A mixed estimator nonparametric regression (MENR) model is an additive model that involves a combination of two estimators or more in multivariable nonparametric regression. The model is used when there are differences in data patterns among predictor variables. This study proposes the development of the MENR model on longitudinal data namely a mixed truncated spline-local linear nonparametric regression (MTSLLNR) model. A modified weighted least square (WLS) method through two-stage estimation is used to estimate the regression function in the proposed model. To illustrate the performance of the MTSLLNR model, a simulation study with a sample size variation of subjects and time points is provided. Additionally, the MTSLLNR model is also applied to model the poverty gap index data. Both simulated and real data results suggest that the proposed model has consistency findings and good performance in longitudinal data modeling. Some highlights of the proposed method are:•The method combines two estimators of local linear and truncated spline to accommodate the differences in data patterns in the nonparametric regression for longitudinal data.•Selection of optimal knots and bandwidth using the generalized cross-validation (GCV) method.•The consistency findings and general performance of the method is shown by simulation and real data application.

Keywords: Generalized cross-validation (GCV); Local linear; Longitudinal data; MENR Model; Mixed Truncated Spline-Local Linear Nonparametric Regression (MTSLLNR) for Longitudinal Data; Truncated Spline; Two-stage estimation.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Image, graphical abstract
Graphical abstract
Fig 1
Fig. 1
Scatter plot of the simulation data for n=5,L=50.
Fig 2
Fig. 2
Plot of the estimation results for the five subjects.
Fig 3
Fig. 3
Scatter plot between the response variable and predictor variables.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Wahba G. SIAM, Society for Industrial and Applied Mathematics; Philadelphia, PA, USA: 1990. Spline Models for Observational Data.
    1. Zulkifly M.I.E., Wahab A.F., Zakaria R. B-Spline curve interpolation model by using intuitionistic fuzzy approach. IAENG Int. J. Appl. Math. 2020;50:1–7.
    1. Montoya E.L., Ulloa N., Miller V. A simulation study comparing knot selection methods with equally spaced knots in a penalized regression spline. Int. J. Stat. Prob. 2014;3:96–110. doi: 10.5539/ijsp.v3n3p96. - DOI
    1. Kayri M., Zirhlioglu G. Kernel smoothing function and choosing bandwidth for non-parametric regression methods. Ozean J. Appl. Sci. 2009;2:49–54.
    1. Zhao G., Ma Y. Robust nonparametric kernel regression estimator. Stat. Probab. Lett. 2016;116:72–79. doi: 10.1016/j.spl.2016.04.010. - DOI

LinkOut - more resources