Optimal bailout strategies resulting from the drift controlled supercooled Stefan problem

Abstract

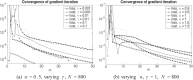
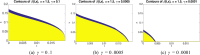
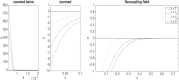
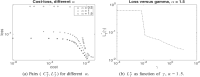
We consider the problem faced by a central bank which bails out distressed financial institutions that pose systemic risk to the banking sector. In a structural default model with mutual obligations, the central agent seeks to inject a minimum amount of cash in order to limit defaults to a given proportion of entities. We prove that the value of the central agent's control problem converges as the number of defaultable institutions goes to infinity, and that it satisfies a drift controlled version of the supercooled Stefan problem. We compute optimal strategies in feedback form by solving numerically a regularized version of the corresponding mean field control problem using a policy gradient method. Our simulations show that the central agent's optimal strategy is to subsidise banks whose equity values lie in a non-trivial time-dependent region.

Keywords: Bail-outs; Mean field control; Propagation of chaos; Supercooled Stefan problem; Systemic risk.

Fig. 1

Convergence of C and L in the PGM for varying $\gamma$ and $\alpha$. Shown are $|L^{(m+1)}-L^{(m)}|$ and $|C^{(m+1)}-C^{(m)}|$

Fig. 2

Contour plots of $(t,x)\to {\beta }^{\star }(t,x)$ for $\alpha =1.5$ and different $\gamma$. The white region is $\{{\beta }^{\star }\le 0.05b_{max}\}$, the (yellow) shaded region $\{{\beta }^{\star }\ge 0.95b_{max}\}$, the dark (blue) zone the transition

Fig. 3

Loss for $\gamma \in \{0.1,0.005,0.001\}$

Fig. 4

Control regions for different $b_{max}$

Fig. 5

Parameters $\alpha =1.5$, $\gamma =0.1$. Left: Density $p(t,·)$ for small negative x. Right: Density $p(t,·)$ in macroscopic range

Fig. 6

Parameters $\alpha =1.5$, $\gamma =0.0005$. Left and middle: Decoupling field $u(t,·)$ for different t and two ranges of (small) x. Right: Decoupling field $u(t,·)$ for different t and marcroscopic range

Fig. 7

Cost $C_T^{\star }$ and loss $L_T^{\star }$ in the optimal regime for logarithmically spaced $\gamma \in [0.0001,0.1]$ and different $\alpha$ in a and the dependence of the losses on $\gamma$ in b

Fig. 8

Cost-loss pairs $(C_T^{\star },L_T^{\star })$ under optimal strategy compared to those for a constant strategy, $(C_T^{\text{u}},L_T^{\text{u}})$, and front-up strategy, $(C_T^{\text{f}},L_T^{\text{f}})$, for two values of $\alpha$

Fig. 9

Smoothed Dirac delta and its derivatives, for $h={10}^{-3}$

Fig. 10

Convergence of C and L over policy gradient iterations