Predicting optimal mixotrophic metabolic strategies in the global ocean
- PMID: 39671489
- PMCID: PMC11641107
- DOI: 10.1126/sciadv.adr0664
Predicting optimal mixotrophic metabolic strategies in the global ocean
Abstract
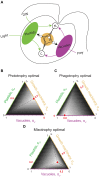
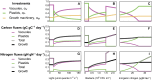
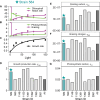
Mixotrophic protists combine photosynthesis with the ingestion of prey to thrive in resource-limited conditions in the ocean. Yet, how they fine-tune resource investments between their two different metabolic strategies remains unclear. Here, we present a modeling framework (Mixotroph Optimal Contributions to Heterotrophy and Autotrophy) that predicts the optimal (growth-maximizing) investments of carbon and nitrogen as a function of environmental conditions. Our model captures a full spectrum of trophic modes, in which the optimal investments reflect zero-waste solutions (i.e., growth is colimited by carbon and nitrogen) and accurately reproduces experimental results. By fitting the model to data for Ochromonas, we were able to predict metabolic strategies at a global scale. We find that high phagotrophic investment is the dominant strategy across different oceanic biomes, used primarily for nitrogen acquisition. Our results therefore support empirical observations of the importance of mixotrophic grazers to upper ocean bacterivory.
Figures

Similar articles
-
Contrasting Mixotrophic Lifestyles Reveal Different Ecological Niches in Two Closely Related Marine Protists.J Phycol. 2020 Feb;56(1):52-67. doi: 10.1111/jpy.12920. Epub 2019 Nov 1. J Phycol. 2020. PMID: 31529498 Free PMC article.
-
Coming to the dark side: How does nitrogen eutrophication reshape the mixotrophic trade-off of osmo-mixotrophy in Ochromonas?Sci Total Environ. 2024 Dec 20;957:177803. doi: 10.1016/j.scitotenv.2024.177803. Epub 2024 Nov 30. Sci Total Environ. 2024. PMID: 39616924
-
Arcobacteraceae are ubiquitous mixotrophic bacteria playing important roles in carbon, nitrogen, and sulfur cycling in global oceans.mSystems. 2024 Jul 23;9(7):e0051324. doi: 10.1128/msystems.00513-24. Epub 2024 Jun 21. mSystems. 2024. PMID: 38904399 Free PMC article.
-
Nutrient ratios as a tracer and driver of ocean biogeochemistry.Ann Rev Mar Sci. 2012;4:113-41. doi: 10.1146/annurev-marine-120709-142821. Ann Rev Mar Sci. 2012. PMID: 22457971 Review.
-
The Minderoo-Monaco Commission on Plastics and Human Health.Ann Glob Health. 2023 Mar 21;89(1):23. doi: 10.5334/aogh.4056. eCollection 2023. Ann Glob Health. 2023. PMID: 36969097 Free PMC article. Review.
References
-
- Worden A. Z., Follows M. J., Giovannoni S. J., Wilken S., Zimmerman A. E., Keeling P. J., Rethinking the marine carbon cycle: Factoring in the multifarious lifestyles of microbes. Science 347, 1257594 (2015). - PubMed
-
- Selosse M.-A., Charpin M., Not F., Mixotrophy everywhere on land and in water: The grand écart hypothesis. Ecol. Lett. 20, 246–263 (2017). - PubMed
-
- Crane K. W., Grover J. P., Coexistence of mixotrophs, autotrophs, and heterotrophs in planktonic microbial communities. J. Theor. Biol. 262, 517–527 (2010). - PubMed
-
- Mitra A., Flynn K. J., Burkholder J. M., Berge T., Calbet A., Raven J. A., Granéli E., Glibert P. M., Hansen P. J., Stoecker D. K., Thingstad F., Tillmann U., Våge S., Wilken S., Zubkov M. V., The role of mixotrophic protists in the biological carbon pump. Biogeosciences 11, 995–1005 (2014).
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

