Virulence Evolution via Pleiotropy in Vector-Borne Plant Pathogens

Abstract

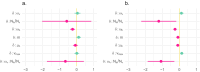
The dynamics of virulence evolution in vector-borne plant pathogens can be complex. Here, we use individual-based, quantitative-genetic simulations to investigate how virulence evolution depends on genetic trade-offs and population structure. Although quite generic, the model is inspired by the ecology of the plant-pathogenic bacterium Xylella fastidiosa, and we use it to gain insights into possible modes of virulence evolution in that group. In particular, we aim to sharpen our intuition about how virulence may evolve over short time scales via antagonistically pleiotropic alleles affecting pathogen performance within hosts and vectors. We find that even when pathogens find themselves much more often in hosts than vectors, selection in the vector environment can cause correlational and potentially non-adaptive changes in virulence in the host. The extent of such correlational virulence evolution depends on many system parameters, including the pathogen transmission rate, the proportion of the pathogen population occurring in hosts, the strengths of selection in host and vector environments, and the functional relationship between pathogen load and virulence. But there is a statistical interaction between the strength of selection in vectors and the proportion of the pathogen population in hosts, such that if within-vector selection is strong enough, over the short term, it can dominate virulence evolution, even when the host environment predominates.

FIGURE 1

Alternative population structures. Network vertices represent specific host (H _i or h _i ) or vector (v _i ) patches. Larger vertices have higher pathogen carrying capacities. Edges represent possible paths for pathogen migration. (a) In the main model, the pathogen population is vector‐borne; migration is only possible between trophic levels, that is, from a host (H _i ) to a vector (v _i ), or vice versa. (b) In an alternative version of the model, migration is unfettered; thus, rather than consisting of a mix of hosts and vectors, the environment consists of a few large and susceptible hosts (H _i ) and several small and tolerant hosts (h _i ).

FIGURE 2

Calculation of the Γ statistic. (a) An example evolutionary path through the phenotype space. For this simulation κ = −0.2, v _max  = 0.3, m = 0.1, K _v  = 20, K _h  = 2000, ɷ _v  = 3.0, ɷ _h  = 3.0, μ _h  = 1e‐4, μ _v  = 0.1, α = 5.0, and ρ = 0.1. (b) That same path translated to start at the origin and rotated so that the ideal path from the origin to the joint phenotypic optimum lies along the x‐axis. (c) Γ is calculated as the sum of deviations from the ideal path, scaled by the length of the path in generations. When Γ is positive, the evolutionary path bends mostly toward the vector environment; conversely when it is negative, the host environment dominates.

FIGURE 3

Summary of multivariate linear models decomposing the variance in (a) T, the log‐transformed number of generations it takes for the pathogen population to evolve a within‐host performance phenotype within 10% of the optimum, and (b) Γ, the degree to which, before T, the pathogen population's evolutionary path bends toward (Γ > 0) or away from (Γ < 0) the vector environment. Points show positive (teal) and negative (magenta) estimated coefficients, and horizontal bars show 95% confidence intervals. All predictors have been centered and scaled to units of standard deviations (the units of the x‐axis).

FIGURE 4

Marginal effect estimates of the interaction between the weakness of selection in vectors, ω _v , and the predominance of hosts N _h /N. Each point and linear interpolation shows the predicted value for T (a) and Γ (b) for a given value of ω _v in combination with a level of N _h /N, where magenta is for −1 SD, teal is for the mean, and gold is for +1 SD.

FIGURE 5

Interactions between dispersal mode (δ) and other predictors of (a) T, the number of generations until a pathogen population evolves a within‐host performance phenotype within 10% of the optimum, and (b) Γ, before T, the degree with which correlation evolution in the pathogen population is dominated by the vector (Γ > 0) or host (Γ < 0) environment. Points show the positive (teal) and negative (magenta) coefficients, and horizontal lines give 95% confidence intervals.

FIGURE 6

Structured equation analysis of model of the evolution of virulence in a vector‐borne pathogen. Edges show positive (teal) and negative (lavender) causal relationships among model parameters (ω _h , ω _v , m, v _max , α) and variables (N _h /N, T, Γ). The width of each edge is in proportion to the magnitude of its effect. Effect coefficients are printed on each edge, followed by its standard error in parentheses.