Beyond-local neural information processing in neuronal networks

Abstract

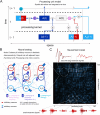
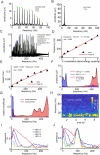
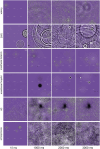
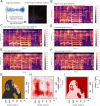
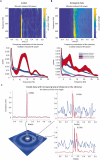
While there is much knowledge about local neuronal circuitry, considerably less is known about how neuronal input is integrated and combined across neuronal networks to encode higher order brain functions. One challenge lies in the large number of complex neural interactions. Neural networks use oscillating activity for information exchange between distributed nodes. To better understand building principles underlying the observation of synchronized oscillatory activity in a large-scale network, we developed a reductionistic neuronal network model. Fundamental building principles are laterally and temporally interconnected virtual nodes (microcircuits), wherein each node was modeled as a local oscillator. By this building principle, the neuronal network model can integrate information in time and space. The simulation gives rise to a wave interference pattern that spreads over all simulated columns in form of a travelling wave. The model design stabilizes states of efficient information processing across all participating neuronal equivalents. Model-specific oscillatory patterns, generated by complex input stimuli, were similar to electrophysiological high-frequency signals that we could confirm in the primate visual cortex during a visual perception task. Important oscillatory model pre-runners, limitations and strength of our reductionistic model are discussed. Our simple scalable model shows unique integration properties and successfully reproduces a variety of biological phenomena such as harmonics, coherence patterns, frequency-speed relationships, and oscillatory activities. We suggest that our scalable model simulates aspects of a basic building principle underlying oscillatory, large-scale integration of information in small and large brains.

Keywords: Columnar architecture; Information integration; Neural network; Neuronal field model; Neuronal oscillations; Parallel computing; Visual perception.

Graphical abstract

Fig. 1

Model outline. (A) The model relies on the unification of activation and inhibition within a virtual oscialltor (node) and the interconnections with neighboring nodes. Three processing steps are central for processing and modulating the model: Δ’(t) (amplitude deviation of the own amplitude à impulse), Δ(t) (integration of impulse à speed) and A(t) (integration of the speed à amplitude or distance). The three processing steps can be modulated by several parameters (a-g). (B) The model represents virtual oscillators and interconnects them laterally. (C) Information is distributed over the entire model and is available at any node over time. Each pixel represents one node (as shown in A and B). The amplitude changes over time can be recorded by different electrode sizes, small electrodes (one node), and big electrodes (many nodes), thus representing the sum of many small electrode recordings (EEG-like signals).

Fig. 2

Wave interference patterns, resonances, and model scaling. (A) Waves emerge from the stimuli locations and propagate through the system, eventually interacting and creating complex interference patterns. Six snapshots display the progression of three internal stimuli (green stars) and two external stimuli (red stars) within the simulation at distinct time points (20 ms, 50 ms, 100 ms, 150 ms, 200 ms, and 250 ms). The evolution illustrates how the stimuli are converted into wave-like signals, and how the resulting interference patterns become increasingly intricate over time. For further details, refer to supplementary videos S1-S11. (B) Frequency analysis of the self-organized signals generated by the model reveals stable resonance frequencies across varying model sizes (3 ×3, 7 ×7, 34 ×34, and 151 ×151 processing units). The four sub-panels provide a comparative view of how model size influences the emergence and stability of these resonances.

Fig. 3

Properties of the model arising from its wave-like dynamics. (A) Periodic stimulation of the model with a 7 Hz peak input (blue cross) generates harmonic responses (green asterisks), highlighting the system's wave-like nature. (B) In contrast, no harmonic generation is observed when the model is stimulated with a 7 Hz sinusoidal input. (C) Upon stimulation with multiple frequencies, the recorded signal from a single processing unit captures both the input frequencies (blue crosses) and their corresponding harmonics (green asterisks). High-frequency (HF) processing is constrained by a sharp upper limit around ∼330 Hz. (D) This upper limit for HF processing shows a linear correlation with the lateral energy coupling parameter (c²). (E) The velocity of wave propagation positively correlates with the capacity for HF coding, which is itself modulated by the amplitude coupling parameter (c²). (F) The parameters (c²) and (f) together define preferred frequency processing domains, corresponding to distinct activity states of the model that simulate different brain states. (G) HF coding is obscured when larger electrodes are used for recording, while smaller electrodes improve the resolution of HF activity. (H) A frequency-time plot reveals a baseline resonance centered around ∼8 Hz, characteristic of the model's simulated waking state. (I-J) Coherence measures of processing unit activity at varying distances (0.5 mm, 2 mm, 3 mm, 8 mm, 16 mm, and 32 mm) demonstrate frequency-specific signal distribution across the model. This is shown under two conditions: (I) when using a chaotic stimulus, and (J) with the addition of a 100 Hz sinusoidal signal.

Fig. 4

Video panel of different states of electric activity reflects biological simulations. By modulating the amplitude transfer within the model (e.g., parameters c², f, g), we can transit between different activity states that we categorize into different simulations of (patho-) physiological states. The screenshots of the visualization of the simulation at different time points give a qualitative impression of the characteristic electric activity of the simulated states. The videos S1-S11 show the full dynamics, fig. S4 shows the related signals and the parameters for the states are given in Table S1.

Fig. 5

Encoding and decoding of songs and images using our model. (A) The conceptual overview illustrates the process where a song (signal length 3000 ms) is downsampled and input into the model. The signal is retrieved from three different locations within the model. An STFT is performed to visualize changes in the frequency spectrum over time. (B) The original signal is displayed, showing frequency components from 0 to 500 Hz over the entire 3000 ms duration. (C) The downsampled signal, maintaining the same time range but with frequencies above 500 Hz filtered out, is shown. (D-F) These panels depict the signals processed by the model at the three different locations indicated in (A). Each processed signal is analyzed and visualized using the STFT, demonstrating the model's ability to preserve the frequency identity from 0 to 500 Hz. Corresponding audio (.wav) files for these signals are available in the supplementary materials (package netlogo/audio). (G) The process begins with a picture that is converted into grey values. Each pixel's grey value is matched with the corresponding node in the model, ensuring that the pixel position aligns with the node position. The grey values are scaled and mapped topographically into the model. (H) The input generates an interference pattern that evolves over time. The figure shows the interference pattern 200 ms after the stimulus onset. This pattern represents the encoded information from the initial image. (I) At any point after the stimulus onset, the original image can be decoded from the interference pattern. The example illustrates the image recovery process at various times after onset. The damping effect, which limits the amplitude over time, influences how long the image can be recovered accurately. For small damping factors, the signal decays at a timescale set by ${\left(f+g\right)}^{-1}$. If the evolution time is much larger than this, it is possible that the signal decays to amplitudes which are comparable to machine precision and consequently the loss of accuracy makes the original image unrecoverable. In this example the damping factors are quite small ($f\sim g\sim 0.001$), and there are no difficulties in recovering the image after approximately 10000 ms.

Fig. 6

Stimulus-locked high-frequency activity shows a slow frequency power modulation after stimulus onset in model and biological data. Analysis of induced and evoked high-frequency activity in microelectrode recordings of macaque V1 neurons responding to visual input (see fig. S9B) and simulated model output to similar input (see fig. S9A). Time-frequency representation (TFR) of induced power is presented: (A) for the model and (B) from biological data. The lower sub-panels show the temporal modulation of HF power (averaged between 250 and 450 Hz) in a frequency plot. The evoked and the induced power change over time was frequency demodulated (FFT) for a prestimulus (purple and cyan) and poststimulus period (blue and red) of 500 ms. Model and biological-induced HF power show a frequency peak around 10 and 20 Hz, indicating a modulation of HF power at this frequency. This modulation is only found for data after stimulus onset. The power values are normalized for comparison. The colored area depicts the SE over trials. (C) This panel shows the temporal evolution of the power (induced - blue and evoked - red) in the 250 - 450 Hz band for simulated electrodes with increasing distance from the stimulus, as shown schematically. The latency of the main power increase is indicated. Time-resolved power for the biological data in comparison to spiking activity, MUA, and gamma power can be found in fig. S11. Induced power corresponds to power measured in the single trial and the averaged over trials. Evoked power refers to the power assessed after averaging over single trials in the time domain, thereby highlighting time-locked changes. TFR is shown with respect to visual stimulus onset (time point 0, relative power change refers to a baseline from −0.6 to