Weak-form inference for hybrid dynamical systems in ecology
- PMID: 39689846
- PMCID: PMC11651893
- DOI: 10.1098/rsif.2024.0376
Weak-form inference for hybrid dynamical systems in ecology
Abstract
Species subject to predation and environmental threats commonly exhibit variable periods of population boom and bust over long timescales. Understanding and predicting such behaviour, especially given the inherent heterogeneity and stochasticity of exogenous driving factors over short timescales, is an ongoing challenge. A modelling paradigm gaining popularity in the ecological sciences for such multi-scale effects is to couple short-term continuous dynamics to long-term discrete updates. We develop a data-driven method utilizing weak-form equation learning to extract such hybrid governing equations for population dynamics and to estimate the requisite parameters using sparse intermittent measurements of the discrete and continuous variables. The method produces a set of short-term continuous dynamical system equations parametrized by long-term variables, and long-term discrete equations parametrized by short-term variables, allowing direct assessment of interdependencies between the two timescales. We demonstrate the utility of the method on a variety of ecological scenarios and provide extensive tests using models previously derived for epizootics experienced by the North American spongy moth (Lymantria dispar dispar).
Keywords: WSINDy; data-driven modelling; hybrid systems; multi-scale model; parameter estimation; system identification.
Conflict of interest statement
The authors declare no competing interests.
Figures
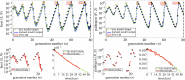
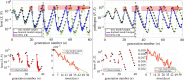

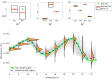
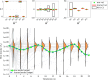









References
-
- Hilborn R, Mangel M. 2013. The ecological detective: confronting models with data (MPB-28). Princeton, NJ: Princeton University Press.
-
- Bolker BM. 2008. Ecological models and data in R. Princeton, NJ: Princeton University Press. (10.1515/9781400840908) - DOI
-
- Burnham KP, Anderson DR. 2007. Model selection and multimodel inference: a practical information-theoretic approach. New York, NY: Springer.
-
- Burnham KP, Anderson DR, Huyvaert KP. 2011. AIC model selection and multimodel inference in behavioral ecology: some background, observations, and comparisons. Behav. Ecol. Sociobiol. 65, 23–35. (10.1007/s00265-010-1029-6) - DOI
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

