Optimal vaccination policy to prevent endemicity: a stochastic model
- PMID: 39694893
- PMCID: PMC11655619
- DOI: 10.1007/s00285-024-02171-z
Optimal vaccination policy to prevent endemicity: a stochastic model
Abstract
We examine here the effects of recurrent vaccination and waning immunity on the establishment of an endemic equilibrium in a population. An individual-based model that incorporates memory effects for transmission rate during infection and subsequent immunity is introduced, considering stochasticity at the individual level. By letting the population size going to infinity, we derive a set of equations describing the large scale behavior of the epidemic. The analysis of the model's equilibria reveals a criterion for the existence of an endemic equilibrium, which depends on the rate of immunity loss and the distribution of time between booster doses. The outcome of a vaccination policy in this context is influenced by the efficiency of the vaccine in blocking transmissions and the distribution pattern of booster doses within the population. Strategies with evenly spaced booster shots at the individual level prove to be more effective in preventing disease spread compared to irregularly spaced boosters, as longer intervals without vaccination increase susceptibility and facilitate more efficient disease transmission. We provide an expression for the critical fraction of the population required to adhere to the vaccination policy in order to eradicate the disease, that resembles a well-known threshold for preventing an outbreak with an imperfect vaccine. We also investigate the consequences of unequal vaccine access in a population and prove that, under reasonable assumptions, fair vaccine allocation is the optimal strategy to prevent endemicity.
Keywords: Age-structured model; Endemicity; Heterogeneous vaccination; Mitigation; Non-Markovian model; Recurrent vaccination; Varying infectiousness and susceptibility; Waning immunity.
© 2024. The Author(s).
Figures
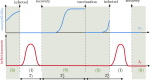
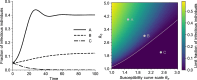
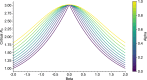
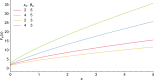
 , on top) and infectiousness (in
, on top) and infectiousness (in  , below) of an individual (color figure online)
, below) of an individual (color figure online)
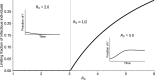
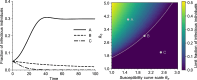
Similar articles
-
Modelling the effect of a booster vaccination on disease epidemiology.J Math Biol. 2006 Mar;52(3):290-306. doi: 10.1007/s00285-005-0356-0. Epub 2005 Nov 10. J Math Biol. 2006. PMID: 16283412
-
Evaluation of vaccination strategies for SIR epidemics on random networks incorporating household structure.J Math Biol. 2018 Jan;76(1-2):483-530. doi: 10.1007/s00285-017-1139-0. Epub 2017 Jun 20. J Math Biol. 2018. PMID: 28634747 Free PMC article.
-
Precise Estimates of Persistence Time for SIS Infections in Heterogeneous Populations.Bull Math Biol. 2018 Nov;80(11):2871-2896. doi: 10.1007/s11538-018-0491-6. Epub 2018 Sep 11. Bull Math Biol. 2018. PMID: 30206808
-
Can the booster interval for the tick-borne encephalitis (TBE) vaccine 'FSME-IMMUN' be prolonged? - A systematic review.Ticks Tick Borne Dis. 2021 Sep;12(5):101779. doi: 10.1016/j.ttbdis.2021.101779. Epub 2021 Jul 13. Ticks Tick Borne Dis. 2021. PMID: 34298356
-
Mathematical models of vaccination.Br Med Bull. 2002;62:187-99. doi: 10.1093/bmb/62.1.187. Br Med Bull. 2002. PMID: 12176860 Review.
References
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

