Numerical study of the effects of minor structures and mean velocity fields in the cerebrospinal fluid flow

Abstract

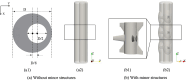
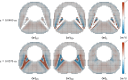
The importance of optimizing intrathecal drug delivery is highlighted by its potential to improve patient health outcomes. Findings from previous computational studies, based on an individual or a small group, may not be applicable to the wider population due to substantial geometric variability. Our study aims to circumvent this problem by evaluating an individual's cycle-averaged Lagrangian velocity field based on the geometry of their spinal subarachnoid space. It has been shown by Lawrence et al. (J Fluid Mech 861:679-720, 2019) that dominant physical mechanisms, such as steady streaming and Stokes drift, are key to facilitating mass transport within the spinal canal. In this study, we computationally modeled pulsatile cerebrospinal fluid flow fields and Lagrangian velocity field within the spinal subarachnoid space. Our findings highlight the essential role of minor structures, such as nerve roots, denticulate ligaments, and the wavy arachnoid membrane, in modulating flow and transport dynamics within the spinal subarachnoid space. We found that these structures can enhance fluid transport. We also emphasized the need for particle tracking in computational studies of mass transport within the spinal subarachnoid space. Our research illuminates the relationship between the geometry of the spinal canal and transport dynamics, characterized by a large upward cycle-averaged Lagrangian velocity zone in the wider region of the geometry, as opposed to a downward zone in the narrower region and areas close to the wall. This highlights the potential for optimizing intrathecal injection protocols by harnessing natural flow dynamics within the spinal canal.

Keywords: Cerebrospinal fluid; Computational fluid dynamics; Intrathecal injection; Lagrangian velocity.

Fig. 1

Two canonical spinal SAS geometries investigated in this paper. a Views of geometry without minor structures. a1 Cross section of the simplified geometry (D = 1.8 cm). a2 The simplified geometry (eccentric annular pipe). b Views of geometry with minor structures. b1 View of the minor structures. b2 The geometry with minor structures

Fig. 2

The axial velocity (w) along the axis of symmetry of the plane at z = 0.04 m at the first diastolic peak for different time step sizes (CC/100, CC/160, CC/200 and CC/267, where ‘CC’ denotes the length of cardiac cycle) and cell sizes (0.36 mm, 0.24 mm, 0.20 mm and 0.14 mm)

Fig. 3

Transient axial velocity (w) fields on the middle plane (z = 0.04 m) of the SAS (without minor structures) spanning across the representative vertebra: a end of diastole, b systolic peak, c end of systole, d diastolic peak

Fig. 4

Transient transverse velocity in the azimuthal direction ($u_{\theta }$) on the middle plane (z = 0.04 m) of the SAS (without minor structures) spanning across the representative vertebra: a end of diastole, b systolic peak, c end of systole, d diastolic peak

Fig. 5

Transient axial velocity (w) fields on the middle plane (z = 0.04 m) of the SAS (with minor structures) spanning across the representative vertebra: a end of diastole, b systolic peak, c end of systole, d diastolic peak

Fig. 6

Transient axial velocity (w) fields and streamlines on a cross section of the SAS (with minor structures) spanning across the representative vertebra. The cross section has a normal vector of [1,1,0] and intersects the point ( $-$0.003 m, $-$0.003 m, 0 m) with respect to the outer circle’s center: a end of diastole, b systolic peak, c end of systole, d diastolic peak

Fig. 7

Axial steady streaming (${⟨w⟩}_{\mathit{SS}}$), cycle-averaged Stokes drift (${⟨w⟩}_{\mathit{SD}}$) and cycle-averaged Lagrangian (${⟨w⟩}_L$) velocity fields on the middle plane (z = 0.0400 m) of the SAS (without minor structures) spanning across the representative vertebra

Fig. 8

Axial steady streaming (${⟨w⟩}_{\mathit{SS}}$), cycle-averaged Stokes drift (${⟨w⟩}_{\mathit{SD}}$) and cycle-averaged Lagrangian (${⟨w⟩}_L$) velocity fields on cross sections (z = 0.0400 m, z = 0.0375 m) of the SAS (with minor structures) spanning across the representative vertebra

Fig. 9

Axial steady streaming velocity field (${⟨w⟩}_{\mathit{SS}}$) on a cross section of the SAS (with minor structures) spanning across the representative vertebra. The cross section has a normal vector of [1,1,0] and intersects the point ( $-$0.003 m, $-$0.003 m, 0 m) with respect to the outer circle’s center

Fig. 10

Cycle-averaged Lagrangian (${⟨w⟩}_L$) velocity field on a cross-sectional plane of the SAS geometry (with minor structures), spanning across the representative vertebra. The cross section, with a normal vector of [1,1,0], intersects the point ($-$0.003 m, $-$0.003 m, 0 m) relative to the center of the outer circle. The field was obtained by interpolating the particle-based velocities to create a continuous representation, providing a smooth depiction of transport dynamics across the plane.

Fig. 11

The plots of the intensity of steady streaming ($Q_{\mathit{SS}}$) within the SAS geometries spanning across the representative vertebra

Fig. 12

The plots of both the average upward and downward steady streaming velocity (${\overline{⟨w⟩}}_{SS,\uparrow }$, ${\overline{⟨w⟩}}_{SS,\downarrow }$), normalized upward and downward cycle-averaged Stokes drift velocities (${\overline{⟨w⟩}}_{SD,\uparrow }$, ${\overline{⟨w⟩}}_{SD,\downarrow }$) and normalized cycle-averaged Lagrangian velocities of particles moving upward and downward (${\overline{⟨w⟩}}_{L,\uparrow }$, ${\overline{⟨w⟩}}_{L,\downarrow }$) within the SAS geometries spanning across the representative vertebra: (a) without minor structures, (b) with minor structures

Fig. 13

The plots of the normalized area of the region with upward steady streaming velocity ($A_{SS,\uparrow }$), upward cycle-averaged Stokes drift velocity ($A_{SD,\uparrow }$), and upward cycle-averaged Lagrangian velocity ($A_{L,\uparrow }$) within the SAS geometries spanning across the representative vertebra: a without minor structures, b with minor structures

Fig. 14

The average of cycle-averaged Lagrangian velocity fields over the Z-axis within the SAS geometries spanning across the representative vertebra: a without minor structures, b with minor structures