DiffMAP-GP: Continuous 2D diffusion maps from particle trajectories without data binning using Gaussian processes
- PMID: 39701212
- PMCID: PMC11959874
- DOI: 10.1016/j.bpr.2024.100194
DiffMAP-GP: Continuous 2D diffusion maps from particle trajectories without data binning using Gaussian processes
Abstract
Diffusion coefficients often vary across regions, such as cellular membranes, and quantifying their variation can provide valuable insight into local membrane properties such as composition and stiffness. Toward quantifying diffusion coefficient spatial maps and uncertainties from particle tracks, we develop a Bayesian framework (DiffMAP-GP) by placing Gaussian process (GP) priors on the family of candidate maps. For sake of computational efficiency, we leverage inducing point methods on GPs arising from the mathematical structure of the data giving rise to nonconjugate likelihood-prior pairs. We analyze both synthetic data, where ground truth is known, as well as data drawn from live-cell single-molecule imaging of membrane proteins. The resulting tool provides an unsupervised method to rigorously map diffusion coefficients continuously across membranes without data binning.
Copyright © 2024 The Authors. Published by Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests V.K., J.S.B., and S.P. declare affiliation with Saguaro AI, an analytics consulting company for the life sciences.
Figures

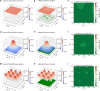
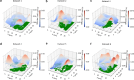
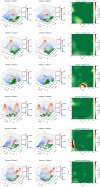


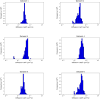
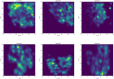

Update of
-
Learning Continuous 2D Diffusion Maps from Particle Trajectories without Data Binning.bioRxiv [Preprint]. 2024 Feb 29:2024.02.27.582378. doi: 10.1101/2024.02.27.582378. bioRxiv. 2024. Update in: Biophys Rep (N Y). 2025 Mar 12;5(1):100194. doi: 10.1016/j.bpr.2024.100194. PMID: 38464131 Free PMC article. Updated. Preprint.
References
-
- Cheng X., Smith J.C. Biological Membrane Organization and Cellular Signaling. Chem. Rev. 2019;119:5849–5880. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

