Invariants for neural automata
- PMID: 39712102
- PMCID: PMC11655788
- DOI: 10.1007/s11571-023-09977-5
Invariants for neural automata
Abstract
Computational modeling of neurodynamical systems often deploys neural networks and symbolic dynamics. One particular way for combining these approaches within a framework called vector symbolic architectures leads to neural automata. Specifically, neural automata result from the assignment of symbols and symbol strings to numbers, known as Gödel encoding. Under this assignment, symbolic computation becomes represented by trajectories of state vectors in a real phase space, that allows for statistical correlation analyses with real-world measurements and experimental data. However, these assignments are usually completely arbitrary. Hence, it makes sense to address the problem which aspects of the dynamics observed under a Gödel representation is intrinsic to the dynamics and which are not. In this study, we develop a formally rigorous mathematical framework for the investigation of symmetries and invariants of neural automata under different encodings. As a central concept we define patterns of equality for such systems. We consider different macroscopic observables, such as the mean activation level of the neural network, and ask for their invariance properties. Our main result shows that only step functions that are defined over those patterns of equality are invariant under symbolic recodings, while the mean activation, e.g., is not. Our work could be of substantial importance for related regression studies of real-world measurements with neurosymbolic processors for avoiding confounding results that are dependant on a particular encoding and not intrinsic to the dynamics.
Keywords: Computational cognitive neurodynamics; Invariants; Language processing; Neural automata; Observables; Symbolic dynamics.
© The Author(s) 2023.
Figures
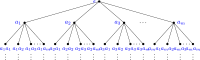
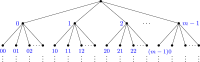
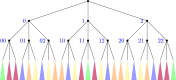


Similar articles
-
A modular architecture for transparent computation in recurrent neural networks.Neural Netw. 2017 Jan;85:85-105. doi: 10.1016/j.neunet.2016.09.001. Epub 2016 Sep 24. Neural Netw. 2017. PMID: 27814468
-
A dynamical systems perspective on the relationship between symbolic and non-symbolic computation.Cogn Neurodyn. 2009 Dec;3(4):415-27. doi: 10.1007/s11571-009-9099-8. Epub 2009 Nov 7. Cogn Neurodyn. 2009. PMID: 19898957 Free PMC article.
-
Symbolic functions from neural computation.Philos Trans A Math Phys Eng Sci. 2012 Jul 28;370(1971):3543-69. doi: 10.1098/rsta.2011.0334. Philos Trans A Math Phys Eng Sci. 2012. PMID: 22711873
-
Predictive landscapes hidden beneath biological cellular automata.J Biol Phys. 2021 Dec;47(4):355-369. doi: 10.1007/s10867-021-09592-7. Epub 2021 Nov 5. J Biol Phys. 2021. PMID: 34739687 Free PMC article. Review.
-
Role of chaotic dynamics in neural plasticity.Prog Brain Res. 1994;102:319-33. doi: 10.1016/S0079-6123(08)60549-X. Prog Brain Res. 1994. PMID: 7800822 Review.
References
-
- Amari SI (1974) A method of statistical neurodynamics. Kybernetik 14:201–215 - PubMed
-
- Anderson JR, Bothell D, Byrne MD, Douglass S, Lebiere C, Qin Y (2004) An integrated theory of the mind. Psychol Rev 111(4):1036–1060 - PubMed
-
- Arbib MA (ed) (1995) The handbook of brain theory and neural networks. MIT Press, Cambridge
-
- Arbib MA, Caplan D (1979) Neurolinguistics must be computational. Behav Brain Sci 2(03):449–460
-
- Atmanspacher H, Beim Graben P (2007) Contextual emergence of mental states from neurodynamics. Chaos Complexity Lett 2(2/3):151–168
LinkOut - more resources
Full Text Sources
Research Materials

