Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Dec 23;19(12):e0315740.
doi: 10.1371/journal.pone.0315740. eCollection 2024.

DC algorithm for estimation of sparse Gaussian graphical models

Tomokaze Shiratori  1 , Yuichi Takano  2
Affiliations

DC algorithm for estimation of sparse Gaussian graphical models

Tomokaze Shiratori et al. PLoS One. .

Abstract

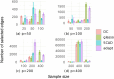
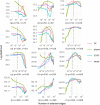
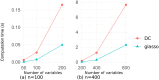
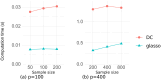
Sparse estimation of a Gaussian graphical model (GGM) is an important technique for making relationships between observed variables more interpretable. Various methods have been proposed for sparse GGM estimation, including the graphical lasso that uses the ℓ1 norm regularization term, and other methods that use nonconvex regularization terms. Most of these methods approximate the ℓ0 (pseudo) norm by more tractable functions; however, to estimate more accurate solutions, it is preferable to directly use the ℓ0 norm for counting the number of nonzero elements. To this end, we focus on sparse estimation of GGM with the cardinality constraint based on the ℓ0 norm. Specifically, we convert the cardinality constraint into an equivalent constraint based on the largest-K norm, and reformulate the resultant constrained optimization problem into an unconstrained penalty form with a DC (difference of convex functions) representation. To solve this problem efficiently, we design a DC algorithm in which the graphical lasso algorithm is repeatedly executed to solve convex optimization subproblems. Experimental results using two synthetic datasets show that our method achieves results that are comparable to or better than conventional methods for sparse GGM estimation. Our method is particularly advantageous for selecting true edges when cross-validation is used to determine the number of edges. Moreover, our DC algorithm converges within a practical time frame compared to the graphical lasso.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Graphs of the regularization terms.
Fig 2
Fig 2. Examples of ground-truth graph structures with (p, n≠0) = (10, 10).
Fig 3
Fig 3. F1 score of edges selected through cross-validation on the random graph dataset.
Fig 4
Fig 4. Number of edges selected through cross-validation on the random graph dataset.
Fig 5
Fig 5. Log-likelihood as a function of the number of selected edges on the random graph dataset (black dashed line: The true number of edges).
Fig 6
Fig 6. F1 score of edges selected through cross-validation on the chain graph dataset.
Fig 7
Fig 7. Number of edges selected through cross-validation on the chain graph dataset.
Fig 8
Fig 8. Log-likelihood as a function of the number of selected edges on the chain graph dataset (black dashed line: The true number of edges).
Fig 9
Fig 9. F1 score of a given number of selected edges on the random graph dataset.
Fig 10
Fig 10. F1 score of a given number of selected edges on the chain graph dataset.
Fig 11
Fig 11. Computation time as a function of the number of variables on the random graph dataset.
Fig 12
Fig 12. Computation time as a function of the number of variables on the chain graph dataset.
Fig 13
Fig 13. Computation time as a function of the sample size on the random graph dataset.
Fig 14
Fig 14. Computation time as a function of the sample size on the chain graph dataset.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Ortiz A, Munilla J, Álvarez-Illán I, Górriz JM, Ramírez J, Alzheimer’s Disease Neuroimaging Initiative. Exploratory graphical models of functional and structural connectivity patterns for Alzheimer’s Disease diagnosis. Frontiers in Computational Neuroscience. 2015;9:132. doi: 10.3389/fncom.2015.00132 - DOI - PMC - PubMed
    1. Idé T, Lozano AC, Abe N, Liu Y. Proximity-based anomaly detection using sparse structure learning. In: Proceedings of the 2009 SIAM International Conference on Data Mining; 2009. p. 97–108.
    1. Tan C, Lee L, Tang J, Jiang L, Zhou M, Li P. User-level sentiment analysis incorporating social networks. In: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2011. p. 1397–1405.
    1. Fan J, Liao Y, Liu H. An overview of the estimation of large covariance and precision matrices. The Econometrics Journal. 2016;19(1):C1–C32. doi: 10.1016/j.jeconom.2018.04.002 - DOI
    1. Drton M, Maathuis MH. Structure learning in graphical modeling. Annual Review of Statistics and Its Application. 2017;4(1):365–393. doi: 10.1146/annurev-statistics-060116-053803 - DOI

LinkOut - more resources