Image-to-mesh conversion method for multi-tissue medical image computing simulations
- PMID: 39717418
- PMCID: PMC11666122
- DOI: 10.1007/s00366-024-02023-w
Image-to-mesh conversion method for multi-tissue medical image computing simulations
Abstract
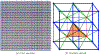
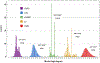
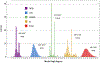
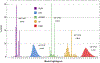
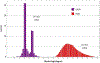
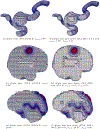
Converting a three-dimensional medical image into a 3D mesh that satisfies both the quality and fidelity constraints of predictive simulations and image-guided surgical procedures remains a critical problem. Presented is an image-to-mesh conversion method called CBC3D. It first discretizes a segmented image by generating an adaptive Body-Centered Cubic (BCC) mesh of high-quality elements. Next, the tetrahedral mesh is converted into a mixed-element mesh of tetrahedra, pentahedra, and hexahedra to decrease element count while maintaining quality. Finally, the mesh surfaces are deformed to their corresponding physical image boundaries, improving the mesh's fidelity. The deformation scheme builds upon the ITK open-source library and is based on the concept of energy minimization, relying on a multi-material point-based registration. It uses non-connectivity patterns to implicitly control the number of extracted feature points needed for the registration and, thus, adjusts the trade-off between the achieved mesh fidelity and the deformation speed. We compare CBC3D with four widely used and state-of-the-art homegrown image-to-mesh conversion methods from industry and academia. Results indicate that the CBC3D meshes (i) achieve high fidelity, (ii) keep the element count reasonably low, and (iii) exhibit good element quality.
Keywords: Image-to-mesh conversion; Medical imaging; Mesh generation; Segmentation.
Figures


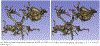
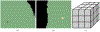
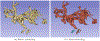







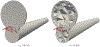
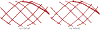



Similar articles
-
TETRAHEDRAL MESH GENERATION FOR MEDICAL IMAGES WITH MULTIPLE REGIONS USING ACTIVE SURFACES.Proc IEEE Int Symp Biomed Imaging. 2010 Apr 14;2010:436-439. doi: 10.1109/ISBI.2010.5490317. Proc IEEE Int Symp Biomed Imaging. 2010. PMID: 21278816 Free PMC article.
-
Adaptive Physics-Based Non-Rigid Registration for Immersive Image-Guided Neuronavigation Systems.Front Digit Health. 2021 Feb 18;2:613608. doi: 10.3389/fdgth.2020.613608. eCollection 2020. Front Digit Health. 2021. PMID: 34713074 Free PMC article.
-
Feature-Sensitive Tetrahedral Mesh Generation with Guaranteed Quality.Comput Aided Des. 2012 May 1;44(5):400-412. doi: 10.1016/j.cad.2012.01.002. Comput Aided Des. 2012. PMID: 22328787 Free PMC article.
-
Automatic reconstruction of a patient-specific high-order surface representation and its application to mesh generation for CFD calculations.Med Biol Eng Comput. 2008 Nov;46(11):1069-83. doi: 10.1007/s11517-008-0390-3. Epub 2008 Sep 16. Med Biol Eng Comput. 2008. PMID: 18795356 Review.
-
Future perspectives for intraoperative MRI.Neurosurg Clin N Am. 2005 Jan;16(1):201-13. doi: 10.1016/j.nec.2004.07.011. Neurosurg Clin N Am. 2005. PMID: 15561539 Review.
References
-
- Archip N, Fedorov A, Lloyd B, Chrisochoides N, Golby A, Black PM, Warfield SK: Integration of patient specific modeling and advanced image processing techniques for image-guided neurosurgery. In: Cleary KR, Galloway J Robert L (eds.) Medical Imaging 2006: Visualization, Image-Guided Procedures, and Display. Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, vol. 6141, pp. 422–429 (2006). 10.1117/12.653930 - DOI
-
- Talos I, Archip N: Volumetric non-rigid registration for MRI-guided brain tumor surgery. Technical report, Surgical Planning Laboratory, Department of Radiology, Brigham and Women’s Hospital, Harvard Medical School; (2007)
-
- Archip N, Clatz O, Whalen S, Kacher D, Fedorov A, Kot A, Chrisochoides N, Jolesz F, Golby A, Black PM, Warfield SK: Non-rigid alignment of pre-operative MRI, fMRI, and DT-MRI with intra-operative MRI for enhanced visualization and navigation in image-guided neurosurgery. NeuroImage 35(2), 609–624 (2007) 10.1016/j.neuroimage.2006.11.060 - DOI - PMC - PubMed
-
- Drakopoulos F, Ortiz R, Enquobahrie A, Sasaki-Adams D, Chrisochoides N: Tetrahedral image-to-mesh conversion software for anatomic modeling of arteriovenous malformations. Procedia Engineering 124, 278–290 (2015) 10.1016/j.proeng.2015.10.139. 24th International Meshing Roundtable - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
