Companion-based multi-level finite element method for computing multiple solutions of nonlinear differential equations
- PMID: 39726586
- PMCID: PMC11671158
- DOI: 10.1016/j.camwa.2024.05.035
Companion-based multi-level finite element method for computing multiple solutions of nonlinear differential equations
Abstract
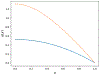
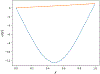
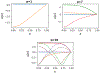
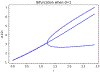
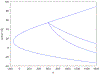
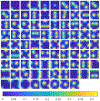
The utilization of nonlinear differential equations has resulted in remarkable progress across various scientific domains, including physics, biology, ecology, and quantum mechanics. Nonetheless, obtaining multiple solutions for nonlinear differential equations can pose considerable challenges, particularly when it is difficult to find suitable initial guesses. To address this issue, we propose a pioneering approach known as the Companion-Based Multilevel Finite Element Method (CBMFEM). This novel technique efficiently and accurately generates multiple initial guesses for solving nonlinear elliptic semi-linear equations containing polynomial nonlinear terms through the use of finite element methods with conforming elements. As a theoretical foundation of CBMFEM, we present an appropriate and new concept of the isolated solution to the nonlinear elliptic equations with multiple solutions. The newly introduced concept is used to establish the inf-sup condition for the linearized equation around the isolated solution. Furthermore, it is crucially used to derive a theoretical error analysis of finite element methods for nonlinear elliptic equations with multiple solutions. A number of numerical results obtained using CBMFEM are then presented and compared with a traditional method. These not only show the CBMFEM's superiority, but also support our theoretical analysis. Additionally, these results showcase the effectiveness and potential of our proposed method in tackling the challenges associated with multiple solutions in nonlinear differential equations with different types of boundary conditions.
Keywords: Boundary conditions; Elliptic semilinear PDEs; Finite element method; Multiple solutions; Nonlinear ODEs.
Figures
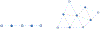
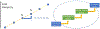
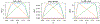
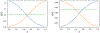



Similar articles
-
Newton Informed Neural Operator for Solving Nonlinear Partial Differential Equations.Adv Neural Inf Process Syst. 2024 Dec;37:120832-120860. Adv Neural Inf Process Syst. 2024. PMID: 40196134 Free PMC article.
-
Simple Equations Method (SEsM): An Effective Algorithm for Obtaining Exact Solutions of Nonlinear Differential Equations.Entropy (Basel). 2022 Nov 14;24(11):1653. doi: 10.3390/e24111653. Entropy (Basel). 2022. PMID: 36421510 Free PMC article. Review.
-
A high-resolution fuzzy transform combined compact scheme for 2D nonlinear elliptic partial differential equations.MethodsX. 2023 Apr 29;10:102206. doi: 10.1016/j.mex.2023.102206. eCollection 2023. MethodsX. 2023. PMID: 37206645 Free PMC article.
-
Can physics-informed neural networks beat the finite element method?IMA J Appl Math. 2024 May 23;89(1):143-174. doi: 10.1093/imamat/hxae011. eCollection 2024 Jan. IMA J Appl Math. 2024. PMID: 38933736 Free PMC article.
-
A fourth-order arithmetic average compact finite-difference method for nonlinear singular elliptic PDEs on a 3D smooth quasi-variable grid network.MethodsX. 2023 Oct 9;11:102424. doi: 10.1016/j.mex.2023.102424. eCollection 2023 Dec. MethodsX. 2023. PMID: 37846352 Free PMC article. Review.
Cited by
-
An Efficient Quasi-Newton Method with Tensor Product Implementation for Solving Quasi-Linear Elliptic Equations and Systems.J Sci Comput. 2025;103(3):89. doi: 10.1007/s10915-025-02897-y. Epub 2025 Apr 30. J Sci Comput. 2025. PMID: 40321660 Free PMC article.
-
On pattern formation in the thermodynamically-consistent variational Gray-Scott model.Math Biosci. 2025 Jul;385:109453. doi: 10.1016/j.mbs.2025.109453. Epub 2025 Apr 30. Math Biosci. 2025. PMID: 40316163 Free PMC article.
-
Newton Informed Neural Operator for Solving Nonlinear Partial Differential Equations.Adv Neural Inf Process Syst. 2024 Dec;37:120832-120860. Adv Neural Inf Process Syst. 2024. PMID: 40196134 Free PMC article.
References
-
- Babuska Ivo, Survey lectures on the mathematical foundations of the finite element method, in: The Mathematical Foundations of the Finite Element Method with Applications to Partial Differential Equations, 1972, pp. 3–359.
-
- Bates Daniel J., Sommese Andrew J., Hauenstein Jonathan D., Wampler Charles W., Numerically Solving Polynomial Systems with Bertini, SIAM, 2013.
-
- Brandt Achi, Livne Oren E., Multigrid Techniques: 1984 Guide with Applications to Fluid Dynamics, revised edition, SIAM, 2011.
-
- Brenner Susanne C., Scott Ridgway, The Mathematical Theory of Finite Element Methods, vol. 15, Springer Science & Business Media, 2008.
-
- Breuer B, Joseph McKenna P, Plum Michael, Multiple solutions for a semilinear boundary value problem: a computational multiplicity proof, J. Differ. Equ 195 (1) (2003) 243–269.
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
