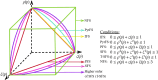
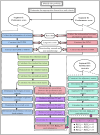
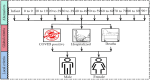
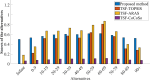Fuzzy APPSS: A novel method for quantifying COVID-19 impact in India under triangular spherical fuzzy environment
- PMID: 39730608
- PMCID: PMC11681153
- DOI: 10.1038/s41598-024-82046-x
Fuzzy APPSS: A novel method for quantifying COVID-19 impact in India under triangular spherical fuzzy environment
Abstract
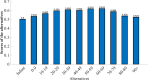
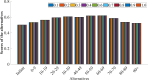
In the current scenario, decision-making models are essential for analyzing real-world problems. To address the dynamic nature of these problems, fuzzy decision-making models have been proposed by various researchers. However, an advanced technique is needed to assess uncertainty in real-time complex situations. Therefore, an association between preference and performance with satisfactory score (APPSS) method is introduced as a fuzzy decision-making method that incorporates two components: preference and performance. This method focuses on demonstrating a connection between preference and performance with a satisfactory measure. Preference analysis evaluates the significance of criteria, while performance analysis assesses the effectiveness of each alternative based on these criteria. Additionally, the satisfactory measure ensures the reliability of the outcomes. The applicability of the proposed method is demonstrated by analyzing the impact of COVID-19 on different age groups in India across various categories. The proposed method employs triangular spherical fuzzy numbers (TSFN), which is a mathematical model that extends beyond conventional fuzzy numbers by incorporating both triangular and spherical characteristics. Furthermore, a new scoring function for TSFN is developed using the graded mean integration method. The analysis reveals that the age group between 60-69 is highly vulnerable to COVID-19. The robustness of these outcomes is verified through sensitivity and comparative analyses. The findings also assist policymakers in more effectively assessing potential future health complications.
Keywords: Fuzzy APPSS method; Preference and performance; Scoring function; Triangular spherical fuzzy number.
© 2024. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare no competing interests. Ethics declarations: This study does not involve research with human participants.
Figures
Similar articles
-
An extended hybrid fuzzy multi-criteria decision model for sustainable and resilient supplier selection.Environ Sci Pollut Res Int. 2022 May;29(25):37291-37314. doi: 10.1007/s11356-021-17851-2. Epub 2022 Jan 20. Environ Sci Pollut Res Int. 2022. PMID: 35050472 Free PMC article.
-
A PROMETHEE based outranking approach for the construction of Fangcang shelter hospital using spherical fuzzy sets.Artif Intell Med. 2023 Jan;135:102456. doi: 10.1016/j.artmed.2022.102456. Epub 2022 Nov 19. Artif Intell Med. 2023. PMID: 36628791
-
A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19.Soft comput. 2023;27(3):1809-1825. doi: 10.1007/s00500-020-05287-8. Epub 2020 Oct 1. Soft comput. 2023. PMID: 33024412 Free PMC article.
-
Decision Support Algorithm for Selecting an Antivirus Mask over COVID-19 Pandemic under Spherical Normal Fuzzy Environment.Int J Environ Res Public Health. 2020 May 13;17(10):3407. doi: 10.3390/ijerph17103407. Int J Environ Res Public Health. 2020. PMID: 32414172 Free PMC article.
-
An Integrated MCDM Model for Conveyor Equipment Evaluation and Selection in an FMC Based on a Fuzzy AHP and Fuzzy ARAS in the Presence of Vagueness.PLoS One. 2016 Apr 12;11(4):e0153222. doi: 10.1371/journal.pone.0153222. eCollection 2016. PLoS One. 2016. PMID: 27070543 Free PMC article. Review.
References
-
- Zadeh, L. A. Fuzzy sets. Information and control8, 338–353 (1965).
-
- Intuitionistic fuzzy sets. Fuzzy Sets and Systems20, 87–96 (1986).
-
- Yager, R. R. Pythagorean membership grades in multicriteria decision making. IEEE Transactions on fuzzy systems22, 958–965 (2013).
-
- Senapati, T. & Yager, R. R. Fermatean fuzzy sets. Journal of ambient intelligence and humanized computing11, 663–674 (2020).
-
- Yager, R. R. Generalized orthopair fuzzy sets. IEEE transactions on fuzzy systems25, 1222–1230 (2016).
MeSH terms
LinkOut - more resources
Full Text Sources
Medical