Measuring age-dependent viscoelasticity of organelles, cells and organisms with time-shared optical tweezer microrheology
- PMID: 39747604
- PMCID: PMC11919717
- DOI: 10.1038/s41565-024-01830-y
Measuring age-dependent viscoelasticity of organelles, cells and organisms with time-shared optical tweezer microrheology
Erratum in
-
Publisher Correction: Measuring age-dependent viscoelasticity of organelles, cells and organisms with time-shared optical tweezer microrheology.Nat Nanotechnol. 2025 May;20(5):708. doi: 10.1038/s41565-025-01901-8. Nat Nanotechnol. 2025. PMID: 40247141 Free PMC article. No abstract available.
Abstract
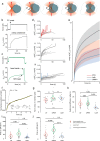
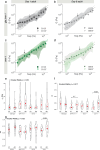
Quantifying the mechanical response of the biological milieu (such as the cell's interior) and complex fluids (such as biomolecular condensates) would enable a better understanding of cellular differentiation and aging and accelerate drug discovery. Here we present time-shared optical tweezer microrheology to determine the frequency- and age-dependent viscoelastic properties of biological materials. Our approach involves splitting a single laser beam into two near-instantaneous time-shared optical traps to carry out simultaneous force and displacement measurements and quantify the mechanical properties ranging from millipascals to kilopascals across five decades of frequency. To create a practical and robust nanorheometer, we leverage both numerical and analytical models to analyse typical deviations from the ideal behaviour and offer solutions to account for these discrepancies. We demonstrate the versatility of the technique by measuring the liquid-solid phase transitions of MEC-2 stomatin and CPEB4 biomolecular condensates, and quantify the complex viscoelastic properties of intracellular compartments of zebrafish progenitor cells. In Caenorhabditis elegans, we uncover how mutations in the nuclear envelope proteins LMN-1 lamin A, EMR-1 emerin and LEM-2 LEMD2, which cause premature aging disorders in humans, soften the cytosol of intestinal cells during organismal age. We demonstrate that time-shared optical tweezer microrheology offers the rapid phenotyping of material properties inside cells and protein blends, which can be used for biomedical and drug-screening applications.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: P.-A.F. is a holder of the US patent no. WO/2022/171898 protecting the time-shared optical tweezer microrheology technique71. X.S. is a cofounder of Nuage Therapeutics. All the remaining authors declare no competing interests.
Figures













References
-
- Hurst, S., Vos, B. E., Brandt, M. & Betz, T. Intracellular softening and increased viscoelastic fluidity during division. Nat. Phys.17, 1270–1276 (2021). - DOI
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Research Materials
Miscellaneous

