Empirical Bayes Linked Matrix Decomposition
- PMID: 39759800
- PMCID: PMC11698509
- DOI: 10.1007/s10994-024-06599-8
Empirical Bayes Linked Matrix Decomposition
Abstract
Data for several applications in diverse fields can be represented as multiple matrices that are linked across rows or columns. This is particularly common in molecular biomedical research, in which multiple molecular "omics" technologies may capture different feature sets (e.g., corresponding to rows in a matrix) and/or different sample populations (corresponding to columns). This has motivated a large body of work on integrative matrix factorization approaches that identify and decompose low-dimensional signal that is shared across multiple matrices or specific to a given matrix. We propose an empirical variational Bayesian approach to this problem that has several advantages over existing techniques, including the flexibility to accommodate shared signal over any number of row or column sets (i.e., bidimensional integration), an intuitive model-based objective function that yields appropriate shrinkage for the inferred signals, and a relatively efficient estimation algorithm with no tuning parameters. A general result establishes conditions for the uniqueness of the underlying decomposition for a broad family of methods that includes the proposed approach. For scenarios with missing data, we describe an associated iterative imputation approach that is novel for the single-matrix context and a powerful approach for "blockwise" imputation (in which an entire row or column is missing) in various linked matrix contexts. Extensive simulations show that the method performs very well under different scenarios with respect to recovering underlying low-rank signal, accurately decomposing shared and specific signals, and accurately imputing missing data. The approach is applied to gene expression and miRNA data from breast cancer tissue and normal breast tissue, for which it gives an informative decomposition of variation and outperforms alternative strategies for missing data imputation.
Keywords: Data integration; dimension reduction; low-rank factorization; missing data imputation; variational Bayes.
Conflict of interest statement
Conflicts of interest/Competing interests None declared.
Figures
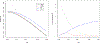


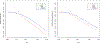
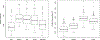
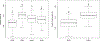

References
-
- Attias H: Inferring parameters and structure of latent variable models by variational Bayes. In: Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence, pp. 21–30. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA: (1999)
-
- Feng Q, Jiang M, Hannig J, Marron J: Angle-based joint and individual variation explained. Journal of multivariate analysis 166, 241–265 (2018)
-
- Fox CW, Roberts SJ: A tutorial on variational Bayesian inference. Artificial intelligence review 38, 85–95(2012)
-
- Gavish M, Donoho DL: Optimal shrinkage of singular values. IEEE Transactions on Information Theory 63(4), 2137–2152 (2017)
Grants and funding
LinkOut - more resources
Full Text Sources
