Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Dec 6;26(12):1061.
doi: 10.3390/e26121061.

Identifying Causal Effects Under Functional Dependencies

Yizuo Chen  1 , Adnan Darwiche  1
Affiliations

Identifying Causal Effects Under Functional Dependencies

Yizuo Chen et al. Entropy (Basel). .

Abstract

We study the identification of causal effects, motivated by two improvements to identifiability that can be attained if one knows that some variables in a causal graph are functionally determined by their parents (without needing to know the specific functions). First, an unidentifiable causal effect may become identifiable when certain variables are functional. Secondly, certain functional variables can be excluded from being observed without affecting the identifiability of a causal effect, which may significantly reduce the number of needed variables in observational data. Our results are largely based on an elimination procedure that removes functional variables from a causal graph while preserving key properties in the resulting causal graph, including the identifiability of causal effects. Our treatment of functional dependencies in this context mandates a formal, systematic, and general treatment of positivity assumptions, which are prevalent in the literature on causal effect identifiability and which interact with functional dependencies, leading to another contribution of the presented work.

Keywords: causal effects; functional dependencies; identifiability.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflicts of interest.

Figures

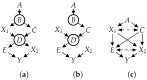
Figure 1
Figure 1
Mutilated and projected graphs of a causal graph. Hidden variables are circled. A bidirected edge (V1⤎⤏V2) is aa compact notation for V1←H→V2, where H is an auxiliary hidden variable. (a) Causal graph; (b) mutilated graph; (c) projected graph.
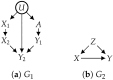
Figure 2
Figure 2
Examples for positivity.
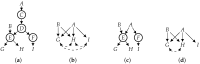
Figure 3
Figure 3
Contrasting projection with functional projection. C and D are functional. Hidden variables are circled. (a) DAG; (b) proj. (a) on A, B, G, H, I; (c) eliminate C,D from (a); (d) proj. (c) on A, B, G, H, I.
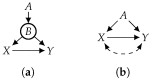
Figure 4
Figure 4
B is functional. (a) DAG; (b) projection.
Figure 5
Figure 5
Variables A,B,C,F,X, and Y are observed. Variables D and E are functional (and hidden). (a) Causal graph; (b) proj. of (a); (c) F-proj. of (a); (d) F-elim. F; (e) F-elim. B.
See this image and copyright information in PMC

References

    1. Pearl J., Mackenzie D. The Book of Why: The New Science of Cause and Effect. Basic Books; New York, NY, USA: 2018.
    1. Pearl J. Causality: Models, Reasoning, and Inference. 2nd ed. Cambridge University Press; Cambridge, UK: 2009.
    1. Pearl J. Causal Diagrams for Empirical Research. Biometrika. 1995;82:669–688. doi: 10.1093/biomet/82.4.669. - DOI
    1. Spirtes P., Glymour C., Scheines R. Causation, Prediction, and Search. 2nd ed. MIT Press; Cambridge, MA, USA: 2000. Adaptive Computation and Machine Learning.
    1. Imbens G.W., Rubin D.B. Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction. Cambridge University Press; Cambridge, UK: 2015.

LinkOut - more resources