Numerical Homogenization of Orthotropic Functionally Graded Periodic Cellular Materials: Method Development and Implementation

Abstract

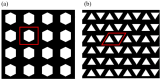
This study advances the state of the art by computing the macroscopic elastic properties of 2D periodic functionally graded microcellular materials, incorporating both isotropic and orthotropic solid phases, as seen in additively manufactured components. This is achieved through numerical homogenization and several novel MATLAB implementations (known in this study as Cellular_Solid, Homogenize_test, homogenize_ortho, and Homogenize_test_ortho_principal). The developed codes in the current work treat each cell as a material point, compute the corresponding cell elasticity tensor using numerical homogenization, and assign it to that specific point. This is conducted based on the principle of scale separation, which is a fundamental concept in homogenization theory. Then, by deriving a fit function that maps the entire material domain, the homogenized material properties are predicted at any desired point. It is shown that this method is very capable of capturing the effects of orthotropy during the solid phase of the material and that it effectively accounts for the influence of void geometry on the macroscopic anisotropies, since the obtained elasticity tensor has different E1 and E2 values. Also, it is revealed that the complexity of the void patterns and the intensity of the void size changes from one cell to another can significantly affect the overall error in terms of the predicted material properties. As the stochasticity in the void sizes increases, the error also tends to increase, since it becomes more challenging to interpolate the data accurately. Therefore, utilizing advanced computational techniques, such as more sophisticated fitting methods like the Fourier series, and implementing machine learning algorithms can significantly improve the overall accuracy of the results. Furthermore, the developed codes can easily be extended to accommodate the homogenization of composite materials incorporating multiple orthotropic phases. This implementation is limited to periodic void distributions and currently supports circular, rectangular, square, and hexagonal void shapes.

Keywords: 2D numerical homogenization; MATLAB code; elasticity tensor; isotropic materials; orthotropic materials; periodic functionally graded cellular materials.

Figure 1

Examples of 2D periodic cellular patterns with parallelogram-shaped unit cells containing (a) hexagonal and (b) triangular voids.

Figure 2

The structure of the FE mesh and its application on a unit cell consisting of two material phases.

Figure 3

(a) An example of geometrically anisotropic cell, (b) An orthotropic periodic cellular structure featuring square voids, printing angle θ, with global x-y and principal 1–2 coordinate systems.

Figure 4

The flowchart of the homogenization process for orthotropic and isotropic solid phase in periodic functionally graded microcellular materials.

Figure 5

Two functionally graded cellular structures with (a) rectangular voids that increase in size in the y-direction and (b) its relative density plot together with (c) a structure with diagonally increasing square voids and (d) the corresponding relative density plot.

Figure 6

Two examples of functionally graded cellular structures with isotropic material phases: (a,b) a diverse circular void pattern and its corresponding relative density plot; (c,d) hexagonal voids and the corresponding relative density plot.

Figure 7

Examples of complex periodic microcellular structures: (a,b) illustrate a medium with circular voids that resembles a waive alongside its corresponding relative density plot; (c,d) present a structure containing random circular voids and its associated relative density plot.

Figure 8

(a) A periodic functionally graded microcellular structure with orthotropy angle of 30° and its associated homogenized material properties including (b) relative density, (c) $E_1$, (d) $E_2$, (e) $G_{12}$, and (f) ${\nu }_{12}$.

Figure 9

(a) A complex periodic microcellular structure with orthotropy angle of 60° and its corresponding homogenized material properties, including (b) relative density, (c) $E_1$, (d) $E_2$, (e) $G_{12}$, and (f) ${\nu }_{12}$.