Performance Tuning of Polarizable Gaussian Multipole Model in Molecular Dynamics Simulations
- PMID: 39772516
- PMCID: PMC11854381
- DOI: 10.1021/acs.jctc.4c01368
Performance Tuning of Polarizable Gaussian Multipole Model in Molecular Dynamics Simulations
Abstract
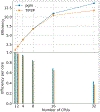
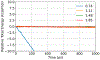
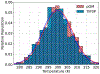
Molecular dynamics (MD) simulations are essential for understanding molecular phenomena at the atomic level, with their accuracy largely dependent on both the employed force field and sampling. Polarizable force fields, which incorporate atomic polarization effects, represent a significant advancement in simulation technology. The polarizable Gaussian multipole (pGM) model has been noted for its accurate reproduction of ab initio electrostatic interactions. In this study, we document our effort to enhance the computational efficiency and scalability of the pGM simulations within the AMBER framework using MPI (message passing interface). Performance evaluations reveal that our MPI-based pGM model significantly reduces runtime and scales effectively while maintaining computational accuracy. Additionally, we investigated the stability and reliability of the MPI implementation under the NVE simulation ensemble. Optimal Ewald and induction parameters for the pGM model are also explored, and its statistical properties are assessed under various simulation ensembles. Our findings demonstrate that the MPI-implementation maintains enhanced stability and robustness during extended simulation times. We further evaluated the model performance under both NVT (constant number, volume, and temperature) and NPT (constant number, pressure, and temperature) ensembles and assessed the effects of varying timesteps and convergence tolerance on induced dipole calculations. The lessons learned from these exercises are expected to help the users to make informed decisions on simulation setup. The improved performance under these ensembles enables the study of larger molecular systems, thereby expanding the applicability of the pGM model in detailed MD simulations.
Conflict of interest statement
The authors declare no competing financial interest.
Figures




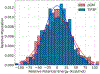

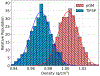
Similar articles
-
Efficient formulation of polarizable Gaussian multipole electrostatics for biomolecular simulations.J Chem Phys. 2020 Sep 21;153(11):114116. doi: 10.1063/5.0019560. J Chem Phys. 2020. PMID: 32962395 Free PMC article.
-
Isotropic Periodic Sum for Polarizable Gaussian Multipole Model.J Chem Theory Comput. 2025 Apr 22;21(8):4040-4050. doi: 10.1021/acs.jctc.5c00123. Epub 2025 Apr 7. J Chem Theory Comput. 2025. PMID: 40194962
-
Stress tensor and constant pressure simulation for polarizable Gaussian multipole model.J Chem Phys. 2022 Mar 21;156(11):114114. doi: 10.1063/5.0082548. J Chem Phys. 2022. PMID: 35317572 Free PMC article.
-
Accounting for electronic polarization in non-polarizable force fields.Phys Chem Chem Phys. 2011 Feb 21;13(7):2613-26. doi: 10.1039/c0cp01971b. Epub 2011 Jan 7. Phys Chem Chem Phys. 2011. PMID: 21212894 Review.
-
CHARMM additive and polarizable force fields for biophysics and computer-aided drug design.Biochim Biophys Acta. 2015 May;1850(5):861-871. doi: 10.1016/j.bbagen.2014.08.004. Epub 2014 Aug 19. Biochim Biophys Acta. 2015. PMID: 25149274 Free PMC article. Review.
References
-
- Halgren TA; Damm W Polarizable force fields. Curr. Opin. Struct. Biol 2001, 11 (2), 236–242. - PubMed
-
- Warshel A; Kato M; Pisliakov AV Polarizable Force Fields: History, Test Cases, and Prospects. J. Chem. Theory Comput 2007, 3 (6), 2034–2045. - PubMed
-
- Lamoureux G; MacKerell AD Jr.; Roux B A simple polarizable model of water based on classical Drude oscillators. J. Chem. Phys 2003, 119 (10), 5185–5197.
-
- Yu H; Hansson T; van Gunsteren WF Development of a simple, self-consistent polarizable model for liquid water. J. Chem. Phys 2003, 118 (1), 221–234.
Grants and funding
LinkOut - more resources
Full Text Sources
