The role of a vaccine booster for a fractional order model of the dynamic of COVID-19: a case study in Thailand

Abstract

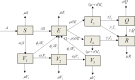
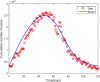
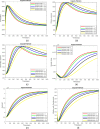
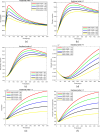
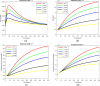
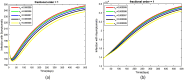
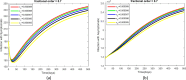
This article addresses the critical need for understanding the dynamics of COVID-19 transmission and the role of booster vaccinations in managing the pandemic. Despite widespread vaccination efforts, the emergence of new variants and the waning of immunity over time necessitate more effective strategies. A fractional-order mathematical model using Caputo-Fabrizio derivatives was developed to analyze the impact of booster doses, symptomatic and asymptomatic infections, and quarantine measures. The model incorporates real epidemic data from Thailand and includes a sensitivity analysis of parameters influencing disease spread. Numerical results indicate that booster vaccinations significantly reduce transmission rates, and the model's predictions align well with the observed data. The basic reproduction number was determined to evaluate disease control, showing that a sustained vaccination campaign, including booster doses, is essential to maintaining immunity and controlling future outbreaks. The findings underscore the importance of ongoing vaccination efforts and provide a robust framework for policymakers to design effective strategies for pandemic control.

Keywords: COVID-19; Caputo-Fabrizio derivatives; Existence and uniqueness; Global stability; Model fitting; Vaccination.

Fig. 1

Shows the relationship of COVID-19 mathematical model.

Fig. 2

The model appropriate to the actual information of COVID-19 spread in Thailand.

Fig. 3

Numerical results are presented for the different fractional orders of the model (4). (a) the number of susceptible populations; (b) the number of populations getting one dose of COVID-19 vaccine; (c) the number of populations getting two doses of COVID-19 vaccine; (d) the number of population getting three doses of COVID-19 vaccine; (e) the number of exposed population; (f) the number of symptomatic population; (g) the number of asymptomatic population; (h) the number of quarantined population; (i) the number of recovered population.

Fig. 3

Numerical results are presented for the different fractional orders of the model (4). (a) the number of susceptible populations; (b) the number of populations getting one dose of COVID-19 vaccine; (c) the number of populations getting two doses of COVID-19 vaccine; (d) the number of population getting three doses of COVID-19 vaccine; (e) the number of exposed population; (f) the number of symptomatic population; (g) the number of asymptomatic population; (h) the number of quarantined population; (i) the number of recovered population.

Fig. 4

Numerical results are presented for the fractional orders of the model (4) for the comparison of the initial number in the population. (a) the number of susceptible populations; (b) the number of population getting one dose of COVID-19 vaccine; (c) the number of population getting two doses of COVID-19 vaccine; (d) the number of population getting three doses of COVID-19 vaccine; (e) the number of exposed population; (f) the number of symptomatic population; (g) the number of asymptomatic population; (h) the number of quarantined population; (i) the number of recovered population, when .

Fig. 4

Numerical results are presented for the fractional orders of the model (4) for the comparison of the initial number in the population. (a) the number of susceptible populations; (b) the number of population getting one dose of COVID-19 vaccine; (c) the number of population getting two doses of COVID-19 vaccine; (d) the number of population getting three doses of COVID-19 vaccine; (e) the number of exposed population; (f) the number of symptomatic population; (g) the number of asymptomatic population; (h) the number of quarantined population; (i) the number of recovered population, when .

Fig. 5

Numerical results were presented for the fractional orders of the model (4) for the comparison of the first dose vaccination rate. (a) the number of susceptible populations; (b) the number of exposed populations; (c) the number of symptomatic populations; (d) the number of asymptomatic populations, when .

Fig. 6

Numerical results were presented for the fractional orders of the model (4) for the comparison of the transmission rate, asymptomatic, infected population. (a) The number of symptomatic populations; (b) the number of asymptomatic populations; when .

Fig. 7

Numerical results were presented for the fractional orders of the model (4) for the comparison of the transmission rate, asymptomatic, infected population. (a) The number of symptomatic populations; (b) the number of asymptomatic populations; when .