Mechanical Cell Interactions on Curved Interfaces
- PMID: 39775998
- PMCID: PMC11706888
- DOI: 10.1007/s11538-024-01406-w
Mechanical Cell Interactions on Curved Interfaces
Abstract
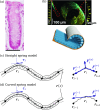
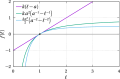
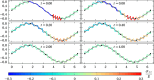
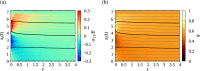
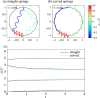
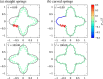
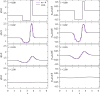
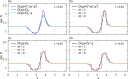
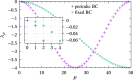
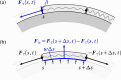
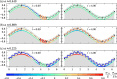
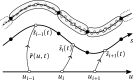
We propose a simple mathematical model to describe the mechanical relaxation of cells within a curved epithelial tissue layer represented by an arbitrary curve in two-dimensional space. This model generalises previous one-dimensional models of flat epithelia to investigate the influence of curvature for mechanical relaxation. We represent the mechanics of a cell body either by straight springs, or by curved springs that follow the curve's shape. To understand the collective dynamics of the cells, we devise an appropriate continuum limit in which the number of cells and the length of the substrate are constant but the number of springs tends to infinity. In this limit, cell density is governed by a diffusion equation in arc length coordinates, where diffusion may be linear or nonlinear depending on the choice of the spring restoring force law. Our results have important implications about modelling cells on curved geometries: (i) curved and straight springs can lead to different dynamics when there is a finite number of springs, but they both converge quadratically to the dynamics governed by the diffusion equation; (ii) in the continuum limit, the curvature of the tissue does not affect the mechanical relaxation of cells within the layer nor their tangential stress; (iii) a cell's normal stress depends on curvature due to surface tension induced by the tangential forces. Normal stress enables cells to sense substrate curvature at length scales much larger than their cell body, and could induce curvature dependences in experiments.
Keywords: Coarse-graining; Diffusion; Mathematical model; Mechanobiology; Surface tension; Tissue growth; Tissue mechanics.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Conflict of interest: Author Prof. Matthew J. Simpson is Editor-in-Chief of the Bulletin of Mathematical Biology. Ethics approval and consent to participate: Not applicable. Consent for publication: All authors gave final approval for publication and agreed to be held accountable for the work performed therein.
Figures

Similar articles
-
Relating cell shape and mechanical stress in a spatially disordered epithelium using a vertex-based model.Math Med Biol. 2018 Mar 16;35(suppl_1):1-27. doi: 10.1093/imammb/dqx008. Math Med Biol. 2018. PMID: 28992197 Free PMC article.
-
Coupling between apical tension and basal adhesion allow epithelia to collectively sense and respond to substrate topography over long distances.Integr Biol (Camb). 2015 Dec;7(12):1611-21. doi: 10.1039/c5ib00240k. Epub 2015 Oct 28. Integr Biol (Camb). 2015. PMID: 26507156 Free PMC article.
-
Nonlinear and nonlocal elasticity in coarse-grained differential-tension models of epithelia.Phys Rev E. 2019 Feb;99(2-1):022411. doi: 10.1103/PhysRevE.99.022411. Phys Rev E. 2019. PMID: 30934282 Free PMC article.
-
Using cell deformation and motion to predict forces and collective behavior in morphogenesis.Semin Cell Dev Biol. 2017 Jul;67:161-169. doi: 10.1016/j.semcdb.2016.07.029. Epub 2016 Aug 2. Semin Cell Dev Biol. 2017. PMID: 27496334 Free PMC article. Review.
-
Peeking into the future: inferring mechanics in dynamical tissues.Biochem Soc Trans. 2024 Dec 19;52(6):2579-2592. doi: 10.1042/BST20230225. Biochem Soc Trans. 2024. PMID: 39656056 Free PMC article. Review.
Cited by
-
Anisotropic persistent random walk model simulates T-cells migration over curved landscapes.Sci Rep. 2025 Jun 4;15(1):19629. doi: 10.1038/s41598-025-02804-3. Sci Rep. 2025. PMID: 40467611 Free PMC article.
References
-
- Alias MA, Buenzli PR (2018) Osteoblasts infill irregular pores under curvature and porosity controls: a hypothesis-testing analysis of cell behaviours. Biomech Model Mechaniobiol 17:1357–1371. 10.1007/s10237-018-1031-x - PubMed
-
- Alias MA, Buenzli PR (2019) A level-set method for the evolution of cells and tissue during curvature-controlled growth. Int J Numer Meth Biomed Engng 2019:e3279. 10.1002/cnm.3279 - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

