Mechanical Cell Interactions on Curved Interfaces

Abstract

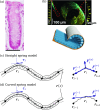
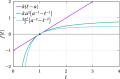
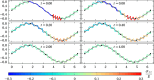
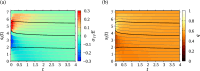
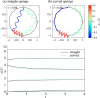
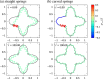
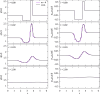
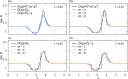
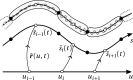
We propose a simple mathematical model to describe the mechanical relaxation of cells within a curved epithelial tissue layer represented by an arbitrary curve in two-dimensional space. This model generalises previous one-dimensional models of flat epithelia to investigate the influence of curvature for mechanical relaxation. We represent the mechanics of a cell body either by straight springs, or by curved springs that follow the curve's shape. To understand the collective dynamics of the cells, we devise an appropriate continuum limit in which the number of cells and the length of the substrate are constant but the number of springs tends to infinity. In this limit, cell density is governed by a diffusion equation in arc length coordinates, where diffusion may be linear or nonlinear depending on the choice of the spring restoring force law. Our results have important implications about modelling cells on curved geometries: (i) curved and straight springs can lead to different dynamics when there is a finite number of springs, but they both converge quadratically to the dynamics governed by the diffusion equation; (ii) in the continuum limit, the curvature of the tissue does not affect the mechanical relaxation of cells within the layer nor their tangential stress; (iii) a cell's normal stress depends on curvature due to surface tension induced by the tangential forces. Normal stress enables cells to sense substrate curvature at length scales much larger than their cell body, and could induce curvature dependences in experiments.

Keywords: Coarse-graining; Diffusion; Mathematical model; Mechanobiology; Surface tension; Tissue growth; Tissue mechanics.

Fig. 1

a Colonic crypt showing a monolayer of epithelial cells in cross section (dark pink); scale bar = 50 $\mathrm{\mu }$m. Reproduced from Dunn et al. (2012) under the terms of the creative commons attribution license; b Epithelial cells on a substrate with transiently induced curvature. Adapted from Schamberger et al. (2023) under the terms of the CC-BY Creative commons attribution 4.0 license (https://creativecommons.org/licenses/by/4.0/); c Straight spring model and d curved spring model of the mechanical interaction between cells along an interface $\mathit{r}(s)$ (solid black line). In this figure, each cell is composed of $m=2$ springs (gray coils). Nodes within a cell are shown as open circles, and nodes connecting two cells are shown as black circles. c The force diagram for the straight spring model shows that restoring forces are directed along the secant line between two nodes on the interface. The normal reaction force ${\mathit{F}}_i^{(\text{n})}$ ensures that the net force is parallel to the unit tangent vector ${\mathit{\tau }}_i$ at node i. d In the curved spring model, the restoring forces ${\mathit{F}}_i^{(\pm )}$ at node i are already parallel to ${\mathit{\tau }}_i$ and so there is no normal reaction force ${\mathit{F}}_i^{(\text{n})}$ (colour figure online)

Fig. 2

Comparison between the Hookean restoring force law $f(\ell )=k(\ell -a)$ (magenta), the nonlinear restoring force law $f(\ell )=k{a}^2(1/a-1/\ell )$ (green), and the nonlinear restoring force law $f(\ell )=(k{a}^3/2)(blue)(1/a^2-1/{\ell }^2)$ ($a=1$, $k=1$ in arbitrary units). The nonlinear restoring force scaling factors are such that their linearisation about the resting spring length $\ell =a$ gives the Hookean restoring force

Fig. 3

Time snapshots of the mechanical relaxation of $N=4$ cells with $m=4$ inner springs (stress-coloured coils) along the open curve $\tilde{\mathit{r}}(u)=(u,Rsin(u))$ (solid black curve) using the curved spring model and a Hookean restoring force. Cell boundaries are shown as black circles. Inner spring boundaries are shown as open circles. The resting spring length is chosen such that the steady state is stress-free; $R=0.8$, $k=4$, $\eta =0.25$, $a\approx 0.45$, $\mathrm{\Delta }t=0.001$ (colour figure online)

Fig. 4

Evolution of spring boundary positions (thin gray lines) and cell boundary positions (thick black lines) in the simulations shown in Fig. 3. Each spring is coloured according to a its tangential stress ${\sigma }_{\tau \tau }({\ell }_i)/E$; and b cell density $q_i$

Fig. 5

Evolution of spring boundary positions along the circle $\mathit{r}(s)=(Rcos(s/R),Rsin(s/R))$ with straight and curved springs, $N=4$, $m=1$, $R=1$, $k=1$, $\eta =1$, $\mathrm{\Delta }t=0.001$. a Initial condition with straight springs of resting length $a=2sin(\pi /4)=\sqrt{2}$; b Initial condition with curved springs of resting length $a=2\pi /4$; c Comparison of the dynamics of mechanical relaxation between straight and curved springs

Fig. 6

Comparison of mechanical relaxation between straight and curved springs on a cross-shaped interface with $N=8$ cells and $m=1$ spring per cell. The interface is defined in polar coordinates by the polar equation $R(\theta )=R_0({cos}^4(\theta )+{sin}^4(\theta ))$; $R_0=1$, $\eta =1$, $k=1$, $\mathrm{\Delta }t=0.001$. The resting length a is chosen such that there is no tangential stress in steady state. The snapshots show the initial configuration ($t=0$) and a mechanically relaxed configuration ($t=100$) for a straight springs with $a\approx 0.7368$; and b curved springs with $a\approx 0.8010$

Fig. 7

Comparison of the evolution of spring boundary positions along the cross-shaped interface of Fig. 6 between straight springs and curved springs with $N=8$ cells. Cell boundaries are shown as solid black line (straight spring model) and thick dashed green lines (curved spring model). Inner spring boundaries within the cells are shown as thin grey lines (straight spring model) and thin dashed green lines (curved spring model). Spring resting lengths are chosen such that there is no tangential stress in steady state. a $m=1$ spring per cell, $k=1$, $\eta =1$, $a\approx 0.7368$ for straight springs, $a\approx 0.8010$ for curved springs, $\mathrm{\Delta }t=0.001$; b $m=8$ springs per cell, $k=8$, $\eta =1/8$, $a\approx 0.0995$ for straight springs, $a\approx 0.1001$ for curved springs, $\mathrm{\Delta }t=0.001$ (colour figure online)

Fig. 8

Comparison of density and stress state between discrete model simulations (magenta) and continuum model simulations (black) for $N=8$ cells around the unit circle with $m=4$ at times $t=0,0.02,0.2,2$ (curved Hookean springs); $R=1$, $k^{\ast }=1$, ${\eta }^{\ast }=1$, $\mathrm{\Delta }t=0.001$. The initial condition considers that one cell boundary is displaced along the circle by half a resting cell length $a^{\ast }=2\pi /8$ such that one cell is initially stretched 50% (${\sigma }_{\tau \tau }/E=-0.5$), and its neighbouring cell is compressed 50% (${\sigma }_{\tau \tau }/E=0.5$), like in Fig. 5b (colour figure online)

Fig. 9

Comparison of cell density relaxation with different restoring forces. The discrete model is solved on a circular interface with curved springs for $N=8$ cells and $m=2,4,8$ springs per cells; $R=1$, $k^{\ast }=1$, ${\eta }^{\ast }=1$, $a^{\ast }=2\pi /8$, $\mathrm{\Delta }t=0.001$. The initial condition is the same for all cases and matches that of Fig. 8 ($t=0$) with one elongated cell adjacent to one compressed cell. Density profile along the interface are shown at time $t=0.05$. a Continuum cell density profiles obtained by solving Eq. (32) with $D(q)=k^{\ast }/({\eta }^{\ast }{q}^2)$, $D(q)=D_0=k^{\ast }{(a^{\ast })}^2/{\eta }^{\ast }\approx 0.62$, and $D(q)=D_0^{\ast }q$, where $D_0^{\ast }=k^{\ast }{(a^{\ast })}^3/{\eta }^{\ast }\approx 0.48$; (b)–(d) Comparison between discrete and continuum model simulations for (b) Hookean springs leading to $D(q)=k^{\ast }/({\eta }^{\ast }{q}^2)$; (b) nonlinear springs leading to linear diffusion $D(q)=D_0$; (c) nonlinear springs leading to porous medium diffusion $D(q)=D_0^{\ast }q$

Fig. 10

Eigenvalues ${\lambda }_p$ of the matrix B corresponding to periodic boundary conditions, $p=0,\dots ,M-1$ (plus signs), and eigenvalues ${\lambda }_p$ of the matrix $\mathcal{B}$ corresponding to fixed boundary conditions, $p=1,\dots ,M-1$ (cross signs), with $M=50$ springs. The inset shows a close-up view of the first eigenvalues. The zero eigenvalue of the matrix B for periodic boundary conditions corresponds to the steady state, see Eq. (46). For fixed boundary conditions, the steady state is not an eigenvector of the matrix $\mathcal{B}$, see Eq. (56)

Fig. 11

Tangential and normal stresses. a Tangential stress ${\sigma }_{\tau \tau }$ is defined as the tangential component of the inner force ${\mathit{F}}_{\tau }$ (blue arrow) divided by the cross-sectional surface area A; b Normal stress ${\sigma }_{\mathit{nn}}$ is defined as the normal component of the inner force ${\mathit{F}}_n$ (large blue arrow) divided by the contact surface area $w\mathrm{\Delta }s$, where w is the cell width in the out-of-plane direction. The normal force ${\mathit{F}}_n$ is the net reaction force exerted by the substrate on the cell between the arc length positions s and $s+\mathrm{\Delta }s$ (small blue arrows). This normal force is induced by the tangential forces on curved portions of the interface only (see text for further detail)

Fig. 12

Tangential and normal stresses along the open curve $\tilde{\mathit{r}}(u)=(u,Rsin(u))$ (solid black curve) using the curved spring model with $N=4,m=4$. Springs are coloured by the tangential stress ${\sigma }_{\tau \tau }/E$. The contact interface between cells and the substrate is coloured by the normal stress ${\sigma }_{\mathit{nn}}/(Eh)$. Simulation parameters are as in Fig. 3, i.e., $R=0.8$, $k=4$, $\eta =0.25$, except resting length a is varied. a $a\approx 0.449$ is such that there is no tangential stress in steady state; b $a\approx 0.899$ is doubled compared to a, resulting in compressive tangential stress in steady state; c $a\approx 0.225$ is halved compared to a, resulting in tensile tangential stress in steady state (colour figure online)

Fig. 13

Time-dependent reparametrisation of the interface. The time-dependent parametrisation $\overline{\mathit{r}}(u,t)$ of the interface $\mathit{r}(s)$ maps constant, evenly spaced coordinates $u_i$ to the time-dependent spring midpoint positions $\mathit{r}({\overline{s}}_i(t))$ (open circles)