Quantum state processing through controllable synthetic temporal photonic lattices

Abstract

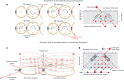
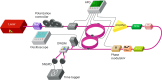
Quantum walks on photonic platforms represent a physics-rich framework for quantum measurements, simulations and universal computing. Dynamic reconfigurability of photonic circuitry is key to controlling the walk and retrieving its full operation potential. Universal quantum processing schemes based on time-bin encoding in gated fibre loops have been proposed but not demonstrated yet, mainly due to gate inefficiencies. Here we present a scalable quantum processor based on the discrete-time quantum walk of time-bin-entangled photon pairs on synthetic temporal photonic lattices implemented on a coupled fibre-loop system. We utilize this scheme to path-optimize quantum state operations, including the generation of two- and four-level time-bin entanglement and the respective two-photon interference. The design of the programmable temporal photonic lattice enabled us to control the dynamic of the walk, leading to an increase in the coincidence counts and quantum interference measurements without recurring to post-selection. Our results show how temporal synthetic dimensions can pave the way towards efficient quantum information processing, including quantum phase estimation, Boson sampling and the realization of topological phases of matter for high-dimensional quantum systems in a cost-effective, scalable and robust fibre-based setup.

Keywords: Fibre optics and optical communications; Quantum optics.

Fig. 1. Illustration of entangled state preparation and quantum interference with the coupled fibre-loop system.

a, A schematic of the four-step process to generate a double-pulse sequence from a single laser pulse. Optical modes can be dynamically gated in and out of each loop. Labels S and L represent the short and long fibre loops, respectively, with ultrafast central couplers in between to couple them. Angular grids inside the loops show the position of the time bins with ~100 ns delay. b, The corresponding spatial network with synthetic position n in the lattice and the number of roundtrips m. It illustrates two roundtrips resulting in four pulses (two per loop) from a single pulse. A step to the left (right) corresponds to light propagation in short (long) loops. c, An artistic depiction of light propagation in the fibre-loop system for a few roundtrips. Light spreads along the synthetic temporal space created by the interloop delay with an increasing number of roundtrips (depicted as different five-level spirals). d, The corresponding DTQW network. With each roundtrip, the complexity of the modal contribution to each time bin, indicated by the colour-coded bullets in both c and d, increases, resulting in different quantum interferences.

Fig. 2. Experimental setup.

A coupler connects two polarization-maintaining fibre loops of 120 m (600 ns) for the long loop and 100 m (500 ns) for the short loop. AFGs dynamically control the coupler’s transmittance. The setup also includes a pulsed laser; an acousto-optic modulator (AOM) to reduce the repetition rate of the laser; PPLN nonlinear crystals to generate photons through SHG and SPDC; phase modulator; wavelength demultiplexer (WDM); oscilloscope; photodetector (PD); and two SNSPDs. The oscilloscope and PDs are used in the classical part of the experiment.

Fig. 3. Two-level quantum interferences.

a,d, Spatial representation of two roundtrips of the DTQW in the coupled fibre-loop system under uncontrolled (a) and controlled (d) schemes. The legend in the centre introduces the action of the three operators used in the experiment (Fourier (50:50), transmission and reflection). b,e, Single-photon histograms obtained through the uncontrolled (b) and controlled (e) schemes. The light-blue box in the single-photon histogram represents the interference coincidence window at zero relative time delay taken from the central interference bin. c,f, Normalized coincidence counts of entangled photons and classical light intensity (blue squares and grey circles, respectively) as a function of the relative phase difference (θ) between the time bins, yielding two-photon quantum interference patterns for the uncontrolled (c) and controlled (f) schemes. Experimental measurements are fitted with theoretical models (blue solid line for entangled qubits and dashed grey line for classical light). From two-photon quantum interference measurements, raw visibility values of V_d=2 = 97.82% and V′_d=2 = 96.83% were extracted for the uncontrolled (c) and controlled (f) schemes, respectively.

Fig. 4. Four-level quantum interferences.

a,c, Spatial representation of four roundtrips of the DTQW in the coupled fibre-loop system under a roundtrip-wise controlled scheme (scheme 1) (a) and roundtrip- and synthetic position-wise controlled scheme (scheme 2) (c). Coincidence counts are measured at the central time bin coincidence window of the fibre loop’s interference output, and at zero photon time delay. b,d, Normalized coincidence counts of four-level entangled photons and classical light intensity (blue squares and grey circles, respectively) as a function of the relative phase difference (θ) between the time bins. Experimental measurements are fitted with theoretical models (solid blue line for entangled qudits and dashed grey line for classical light). From two-photon quantum interference measurements, raw visibility values of V_d=4 = 91.55% and V′_d=4 = 89.61% were extracted for scheme 1 (b) and scheme 2 (d), respectively.