Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Dec 24;5(1):vbae208.
doi: 10.1093/bioadv/vbae208. eCollection 2025.

QOMIC: quantum optimization for motif identification

Hoang M Ngo  1 , Tamim Khatib  1 , My T Thai  1 , Tamer Kahveci  1
Affiliations

QOMIC: quantum optimization for motif identification

Hoang M Ngo et al. Bioinform Adv. .

Abstract

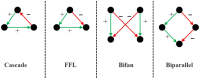
Motivation: Network motif identification (MI) problem aims to find topological patterns in biological networks. Identifying disjoint motifs is a computationally challenging problem using classical computers. Quantum computers enable solving high complexity problems which do not scale using classical computers. In this article, we develop the first quantum solution, called QOMIC (Quantum Optimization for Motif IdentifiCation), to the MI problem. QOMIC transforms the MI problem using a integer model, which serves as the foundation to develop our quantum solution. We develop and implement the quantum circuit to find motif locations in the given network using this model.

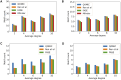
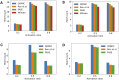
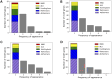
Results: Our experiments demonstrate that QOMIC outperforms the existing solutions developed for the classical computer, in term of motif counts. We also observe that QOMIC can efficiently find motifs in human regulatory networks associated with five neurodegenerative diseases: Alzheimer's, Parkinson's, Huntington's, Amyotrophic Lateral Sclerosis, and Motor Neurone Disease.

Availability and implementation: Our implementation can be found in https://github.com/ngominhhoang/Quantum-Motif-Identification.git.

PubMed Disclaimer

Conflict of interest statement

None declared.

Figures

Figure 1.
Figure 1.
Four possible motif patterns with corresponding regulatory relations used in the synthetic dataset. The green color (or +) represents activation, while the red one (or −) represents repression. The distribution of the activation and repression to the motif edges show one possible configuration. Other configurations with different number and distribution of activation and repressions are also possible.
Figure 2.
Figure 2.
Analysis of the QOMIC and three baseline methods in term of the number of motif embeddings found by varying the number of nodes in the synthetic networks. The analysis is illustrated in four motif types including (A) Cascase, (B) FFL, (C) Bifan, and (D) Biparallel.
Figure 3.
Figure 3.
Analysis of the QOMIC and three baseline methods in term of the number of motif embeddings found by varying the density in the synthetic networks. The analysis is illustrated in four motif types including (A) Cascase, (B) FFL, (C) Bifan, and (D) Biparallel.
Figure 4.
Figure 4.
Analysis of the QOMIC and three baseline methods in term of the number of motif embeddings found by varying the activation ratio in the synthetic networks. The analysis is illustrated in four motif types including (A) Cascase, (B) FFL, (C) Bifan, and (D) Biparallel.
Figure 5.
Figure 5.
The statistics on the number of motif genes with different appearance frequency in five diseases. The first column represents the number of genes exclusively linked to one of five diseases. The statistics are illustrated in four motif types including (A) Cascase, (B) FFL, (C) Bifan, and (D) Biparallel.
See this image and copyright information in PMC

References

    1. Aaronson S, Arkhipov A. The computational complexity of linear optics. In: Proceedings of the Forty-Third Annual ACM Symposium on Theory of Cmputing (STOC’11). New York, NY, USA: Association for Computing Machinery, 2011, 333–42.
    1. Aleksandrowicz G, Alexander T, Kl P et al. Qiskit: An Open-source Framework for Quantum Computing. 2019.
    1. Alon U. Network motifs: theory and experimental approaches. Nat Rev Genet 2007;8:450–61. - PubMed
    1. Boev AS, Rakitko AS, Usmanov SR et al. Genome assembly using quantum and quantum-inspired annealing. Sci Rep 2021;11:13183. - PMC - PubMed
    1. Cerezo M, Arrasmith A, Babbush R et al. Variational quantum algorithms. Nat Rev Phys 2021;3:625–44.

LinkOut - more resources