Error mitigation in brainbox quantum autoencoders

Abstract

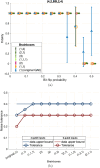
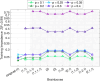
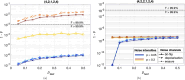
Quantum hardware faces noise challenges that disrupt multiqubit entangled states. Quantum autoencoder circuits with a single qubit bottleneck have demonstrated the capability to correct errors in noisy entangled states. By introducing slightly more complex structures in the bottleneck, referred to as brainboxes, the denoising process can occure more quickly and efficiently in the presence of stronger noise channels. Selecting the most suitable brainbox for the bottleneck involves a trade-off between the intensity of noise on the hardware and training complexity. Finally, by analysing the Rényi entropy flow throughout the networks, we demonstrate that the localization of entanglement plays a central role in denoising through learning.

Fig. 1

Architecture of a typical brainbox quantum autoencoder with symmetric 4-qubit input/output layers and the brainbox of K layers in the middle. The left red subnet encodes the state of input layer on BB by compressing it and the right blue subnet decodes the compressed state on the output layer. BB is represented by the set of qubit numbers in a row from left to right, i.e., . 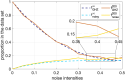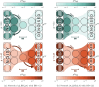For example, (1, 1, 1) means -QAE, (2) is -QAE, and (1, 2) is -QAE.

Fig. 2

The architecture for denoising a GHZ triplet in a BB-QAE, configured as [3, 2, BB, 2, 3] with BB = [2, 2], achieves qubit efficiency through strategic resets during optimization. Each unitary interaction between layers couples marked qubits only. This method minimizes qubit use while maintaining robust denoising capability.

Fig. 3

Training data set: The distribution of 4-qubit GHZ and states other than GHZ in the training set of infinite size in dashed, versus 200 samples size in solid lines. In the infinite size case, the distribution of GHZ for all noise probabilities p dominates, while in the finite set at large p sometimes artefacts prevents the dominancy of GHZ over other states due to strong noise channels.

Fig. 4

(a) Testing fidelity: Average output state fidelity over a range of noisy test states with noise probability p. The error bars indicates the absolute value of standard deviation in the data about average fidelity. When it is large, it indicates that some noise realizations do not reach high fidelity states after denoising while some do. (b) Tolerance thresholds: The noise probability that returns output states with at least 99% fidelity with the ideal GHZ state. Various networks with 4- and 6-qubit input/output layers and different BBs have been tested. Some brainbox bottleneckes make large improvements in the network tolerance threshold.

Fig. 5

Training impedance for the optimization of (4,2,BB,2,4) networks. As the noise intensities grow, the optimization is more demanding. Some BBs show to be less efficient to rapidly gain high fidelity in the output state. These results are robust and remain unchanged for any randomly selected initial mapping, as described before Eq. (5)..

Fig. 6

Cross-tests results for two networks: (4,2,1,2,4) and (4,2,2,1,2,4) associated to (1) and (2,1) brainbox subnetworks. Three noise channels were implemented with noise intensities : the bit-flip channel (full lines), the depolarizing channel (dashed lines) and the erasure channel (dotted lines). The (1)-QAE shows more sensitivity noise in the test states: for the same training probability , the reconstruction error fluctuates and larger errors occur on unfamiliar noise channels. In contrast, the map optimized by the (2,1)-QAE treats all noise channels and intensities equally. The outputs of the BB-QAE lose dependency on the noise it was trained with. In addition, the reconstruction error over the weak noise regime is lower compared to the (1)-QAE.

Fig. 7

Layerwise Rényi entropy . Darker colors indicates larger entropy of noisy mixed states. We study a single-qubit brainbox BB=(1) in (a), and a double-qubit layer brainbox BB=(2) in (b). IN the first rwo on both (a) and (b) single qubit flip probability is and this makes entropy decrease from let to right in the network. In this case one can see noise is localized in the encoder and is blocked away from the brainbox; i.e. this is how both brainboxes can filter out noise at the bottleneck. In the lower rown of (a,b) we consider stronger flip probability than the tolerance of all BB-QAEs, and we see input noise leaks out of the bottleneck to the right side and noise accumulates in the decoder and output layer. For all these evaluations we first initialize the input layer at the training set, then apply the optimum unitary map we trained to denoises the output layer state, and evaluate the density matrix, and finally by tracing out some layers we evaluate entropy of layers. We take average of the entropy by evaluating it at different initial state.