Risky actions: Why and how to estimate variability in motor performance
- PMID: 39842287
- PMCID: PMC11849373
- DOI: 10.1016/j.actpsy.2025.104703
Risky actions: Why and how to estimate variability in motor performance
Abstract
We describe the difficulties of measuring variability in performance, a critical but largely ignored problem in studies of risk perception. The problem seems intractable if a large number of successful and unsuccessful trials are infeasible. We offer a solution based on estimates of task-specific variability pooled across the sample. Using a dataset of adult performance in throwing and walking tasks, we show that mischaracterizing the slope leads to unacceptably large errors in estimates of performance levels that undermine analyses of risk perception. We introduce a "pooled-slope" solution that approximates estimates of individual variability in performance and outperforms arbitrary assumptions about performance variability within and across tasks. We discuss the advantages of objectively measuring performance based on the rate of successful attempts-modeled via psychometric functions-for improving comparisons of risk across participants, tasks, and studies.
Keywords: Affordances; Motor performance; Psychometric; Psychophysics; Risk estimation; Risk perception.
Copyright © 2025 The Authors. Published by Elsevier B.V. All rights reserved.
Conflict of interest statement
Declaration of competing interest John M. Franchak – I have nothing to declare. Christina M. Hospodar – I have nothing to declare. Karen E. Adolph – I have nothing to declare.
Figures
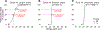



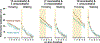
References
-
- Adolph KE (1995). Psychophysical assessment of toddlers’ ability to cope with slopes. Journal of Experimental Psychology: Human Perception and Performance, 21, 734–750. - PubMed

