Dendrites endow artificial neural networks with accurate, robust and parameter-efficient learning
- PMID: 39843414
- PMCID: PMC11754790
- DOI: 10.1038/s41467-025-56297-9
Dendrites endow artificial neural networks with accurate, robust and parameter-efficient learning
Abstract
Artificial neural networks (ANNs) are at the core of most Deep Learning (DL) algorithms that successfully tackle complex problems like image recognition, autonomous driving, and natural language processing. However, unlike biological brains who tackle similar problems in a very efficient manner, DL algorithms require a large number of trainable parameters, making them energy-intensive and prone to overfitting. Here, we show that a new ANN architecture that incorporates the structured connectivity and restricted sampling properties of biological dendrites counteracts these limitations. We find that dendritic ANNs are more robust to overfitting and match or outperform traditional ANNs on several image classification tasks while using significantly fewer trainable parameters. These advantages are likely the result of a different learning strategy, whereby most of the nodes in dendritic ANNs respond to multiple classes, unlike classical ANNs that strive for class-specificity. Our findings suggest that the incorporation of dendritic properties can make learning in ANNs more precise, resilient, and parameter-efficient and shed new light on how biological features can impact the learning strategies of ANNs.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures
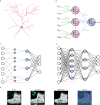
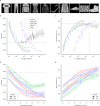
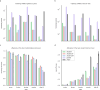
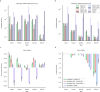
Update of
-
Dendrites endow artificial neural networks with accurate, robust and parameter-efficient learning.ArXiv [Preprint]. 2024 Sep 13:arXiv:2404.03708v2. ArXiv. 2024. Update in: Nat Commun. 2025 Jan 22;16(1):943. doi: 10.1038/s41467-025-56297-9. PMID: 39314509 Free PMC article. Updated. Preprint.
References
-
- Attwell, D. & Laughlin, S. B. An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab.21, 1133–1145 (2001). - PubMed
-
- Luccioni, A. S., Jernite, Y. & Strubell, E. Power hungry processing: watts driving the cost of AI deployment? In Proc.2024 ACM Conference on Fairness, Accountability, and Transparency 85–99 (FACCT, 2024).
-
- Strubell, E., Ganesh, A. & McCallum, A. Energy and policy considerations for deep learning in NLP. In Proc. 57th Annual Meeting of the Association for Computational Linguistics, 3645–3650 (Association for Computational Linguistics, Florence, Italy, 2019).
-
- Mehonic, A. & Kenyon, A. J. Brain-inspired computing needs a master plan. Nature604, 255–260 (2022). - PubMed
-
- McCloskey, M. & Cohen, N. J. Catastrophic interference in connectionist networks: the sequential learning problem. in Psychology of Learning and Motivation vol. 24 109–165 (Elsevier, 1989).
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

