Algorithms for Solving the Equilibrium Composition Model of Arc Plasma

Abstract

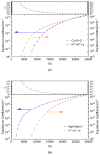
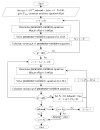
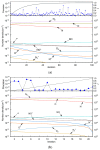
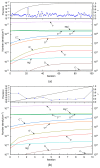
In the present study, the Homotopy Levenberg-Marquardt Algorithm (HLMA) and the Parameter Variation Levenberg-Marquardt Algorithm (PV-LMA), both developed in the context of high-temperature composition, are proposed to address the equilibrium composition model of plasma under the condition of local thermodynamic and chemical equilibrium. This model is essentially a nonlinear system of weakly singular Jacobian matrices. The model was formulated on the basis of the Saha and Guldberg-Waage equations, integrated with Dalton's law of partial pressures, stoichiometric equilibrium, and the law of conservation of charge, resulting in a nonlinear system of equations with a weakly singular Jacobian matrix. This weak singularity primarily arises due to significant discrepancies in the coefficients between the Saha equation and the Guldberg-Waage equation, attributed to differing chemical reaction energies. By contrast, the coefficients in the equations derived from the other three principles within the equilibrium composition model are predominantly single-digit constants, further contributing to the system's weak singularity. The key to finding the numerical solution to nonlinear equations is to set reasonable initial values for the iterative solution process. Subsequently, the principle and process of the HLMA and PV-LMA algorithms are analyzed, alongside an analysis of the unique characteristics of plasma equilibrium composition at high temperatures. Finally, a solving method for an arc plasma equilibrium composition model based on high temperature composition is obtained. The results show that both HLMA and PV-LMA can solve the plasma equilibrium composition model. The fundamental principle underlying the homotopy calculation of the (n-1) -th iteration, which provides a reliable initial value for the n-th LM iteration, is particularly well suited for the solution of nonlinear equations. A comparison of the computational efficiency of HLMA and PV-LMA reveals that the latter exhibits superior performance. Both HLMA and PV-LMA demonstrate high computational accuracy, as evidenced by the fact that the variance of the system of equations ||F|| < 1 × 10^-15. This finding serves to substantiate the accuracy and feasibility of the method proposed in this paper.

Keywords: HLMA; PV–LMA; arc plasma; equilibrium composition model.

Figure 1

Change curve of each equilibrium coefficient with temperature in the air plasma.

Figure 2

Change curve of each equilibrium coefficient with temperature in Mg−CO plasma.

Figure 3

The change curves of the maximum and minimum equilibrium coefficients in the plasma and their ratio q with temperature: (a) air plasma, (b) Mg−CO mixture plasma.

Figure 4

Calculation flow chart of the HLMA algorithm.

Figure 5

Calculation flow chart of PV–LMA algorithm.

Figure 6

The change curves of homotopy factor, accuracy and particle number density of nitrogen plasma with the number of homotopy steps in the two algorithms: (a) HLMA, (b) PV–LMA.

Figure 7

The change curves of homotopy factor, accuracy and particle number density of air plasma with the number of homotopy steps in the two algorithms: (a) HLMA, (b) PV–LMA.

Figure 8

The change curves of plasma homotopy factor, accuracy and particle number density of the mixed Mg50%−CO% 50% plasma with the number of homotopy steps in the two algorithms: (a) HLMA, (b) PV–LMA.

Figure 9

Comparison of the number of calculations required by the HLMA and PV–LMA algorithms.